Student Poster Abstracts
 Amogh Anakru Penn State University  |
Topological Phases and Phase Transitions from Dipolar Symmetry BreakingSystems with dipole moment conservation have been of recent interest, as they realize both novel quantum dynamics and exotic ground state phases. In this work, we study some generic properties of 2-D dipole-conserving fermionic models at integer fillings. We find that a dipolar symmetry-breaking phase can result in a mean-field band insulator whose topological indices can strongly affect the low-energy physics of the dipolar Goldstone modes. The critical theory corresponding to the topological phase transition superficially resembles QED3, but there are key differences which endow this critical point with unusual properties, including a dynamical critical exponent greater than 1. |
|
 Noga Bashan Weizmann Institute of Science  |
Extended strange metal regime from superconducting puddlesWe study a model of mesoscale superconducting puddles in a metal, represented as dynamical impurities interacting with a finite number of electronic channels via Andreev and normal scattering. We identify conditions under which the collection of puddles make a T-linear contribution to the resistivity and a T ln(1/T) to the specific heat and thermopower. This behavior emerges in an intermediate temperature range that extends from an upper energy scale set by the renormalized charging energy of the puddles, and down to an exponentially small scale associated with a charge-Kondo crossover, provided that the number of electronic channels interacting with the puddle is large. The phenomenology of our model resembles the apparent extended strange metal regime observed in overdoped cuprates which exhibits T-linear resistivity at low T over a finite range of doping. |
|
 Marcus Bintz Harvard University |
||
 Sayak Biswas The Ohio State University  |
Andreev versus Tunneling Spectroscopy of Unconventional Flat Band SuperconductorsAndreev spectroscopy is one of the few phase-sensitive experiments done on moiré graphene superconductors (SC) that can shed light on the pairing symmetry. Its interpretation however is unclear, as STM experiments in the Andreev and tunneling regimes show two distinct energy scales whose origin is mysterious. We show using a Green’s function formulation that the two energy scales cannot be understood as a SC gap in the Andreev spectra and a pseudogap in tunneling. We also show that the ballistic Andreev regime can never be realized in moire SCs as the large mismatch in the Fermi velocity vF of the flat band SC and the STM tip renormalizes a transparent interface towards the tunneling regime. We discuss self-energy corrections to vF that determines the conductance. Finally, we model the Andreev experiment as a circular metallic disc embedded in an unconventional SC. With strong vF mismatch the low bias conductance is dominated by tip-induced Andreev bound states, responsible for the low energy scale distinct from the SC gap seen in tunneling. |
|
 Sihan Chen University of Chicago  |
Quantum Bosonization of 2+1D Fermi LiquidDeveloping controlled and efficient approaches to study compressible phases is an important challenge. We compute the non-analytic correction to the density response of a 2+1D Fermi liquid by bosonizing the Fermi surface using the co-adjoint orbit formalism. The non-analytic correction arises naturally as the one-loop correction within the bosonization framework, highlighting the simplicity and efficiency of this approach compared to the conventional fermionic methods, particularly for Fermi liquids with generic Landau parameters. We employ a patch prescription to evaluate the one-loop correction and match it with the result obtained from the fermionic approach for free Fermi gas. Our method can be extended to compute the response function in non-Fermi liquid systems, where strong quantum fluctuation dominates the low-energy regime, making the non-analytic the leading contribution. |
|
 Joshua Covey University of Florida  |
Integrals of products of Bessel functions: a perspective from the physics of umklapp scattering and the application to transport in twisted bilayer grapheneIntegrals of products of Bessel functions exhibit an intriguing feature: they may vanish identically, not due to an orthogonality property, but rather when certain conditions on the parameters specifying the integrand are satisfied. We provide a physical interpretation of this feature in the context of many-body properties of electrons on a lattice (“Bloch electrons”), namely, in terms of the umklapp scattering rate. (In an umklapp event, the change in the momentum of two colliding electrons is equal to a reciprocal lattice vector, which gives rise to a finite resistivity due to electron-electron interaction.) In this context, the vanishing of an integral follows simply from the condition that an umklapp process is kinematically forbidden due to the Fermi surface being smaller than a critical value. Furthermore, we apply these results to transport data for twisted bilayer graphene at small twist angles (but away from the magic angle). We theoretically deduce the temperature scaling behavior for densities above and below the threshold for which umklapp scattering events take place. |
|
 Joseph Cuozzo Sandia National Laboratories  |
Leggett modes and non-reciprocity in a Dirac semimetalTopological materials are a broad class of materials which characteristically host surface states with electronic properties which are distinct from those in the bulk. When a topological material is incorporated into a heterostructure with a superconductor, exotic topological superconducting states can develop at the interface. These states are of fundamental interest since they can exhibit exotic electronic properties such as non-Abelian anyonic exchange, which is also crucial for topological quantum computing. In this poster, we will explore surface-bulk state interplay in topological superconducting heterostructures and discuss how novel phenomena can emerge in these heterostructures. We will first present results on our recent discovery of Leggett collective modes in Dirac semimetals (DSM). We will present a theoretical model for Leggett modes arising in DSM-based Josephson junctions and experimental verification of the mode in cadmium arsenide. Furthermore, our theoretical model predicts the observed signatures of the Leggett modes in cadmium arsenide are associated with a spontaneously broken time-reversal symmetry superconducting state. We present experiment evidence for this exotic state in the form of a zero-field supercurrent diode effect in cadmium arsenide across multiple devices and two different synthesis methods. |
|
 Katherine Ding University of Pennsylvania  |
Quantum geometry tuned magnetic exchange in a Mott insulatorQuantum geometry has recently emerged as an important guiding principle for understanding and engineering properties of quantum materials. While it is well known that a nonzero quantum metric bounds the spread of Wannier orbitals from below, the consequences of this absence of localization are less explored for strongly interacting Mott insulators, whose theory is formulated in terms of exponentially localized Wannier functions. It would therefore be valuable to reconcile these two divergent pictures, and understand how quantum geometry in general affects the competition between correlated phases. In this work, we propose that quantum geometry intrinsic to Bloch wavefunctions can act as a tuning knob for effective magnetic interactions in the presence of strong interactions. We illustrate this proposal by concrete toy models and reveal a competition between ferromagnetism and antiferromagnetism as a function of Wannier function spread, thereby interpolating between the two intuitive pictures of flavor polarization and simple Mott antiferromagnetism. |
|
 Stefan Divic University of California at Berkeley  |
Anyon Superconductivity from Topological Criticality in a Hofstadter-Hubbard ModelWe argue that the combination of strong repulsive interactions and high magnetic fields can generate electron pairing and superconductivity. Inspired by the large lattice constants of moir’e materials, which make large flux per unit cell accessible at laboratory fields, we study the triangular lattice Hofstadter-Hubbard model at one-quarter flux quantum per plaquette, where previous literature has argued that a chiral spin liquid separates a weak-coupling integer quantum Hall phase and a strong-coupling topologically-trivial antiferromagnetic insulator at a density of one electron per site. We argue that topological superconductivity emerges upon doping in the vicinity of the integer quantum Hall to chiral spin liquid transition. We employ exact diagonalization and density matrix renormalization group methods to examine this theoretical scenario and find that electronic pairing indeed occurs on both sides of criticality over a remarkably broad range of interaction strengths. On the chiral spin liquid side, our results provide a concrete model realization of the long-hypothesized mechanism of anyon superconductivity. Our study thus establishes a beyond-BCS mechanism for electron pairing in a well-controlled limit, relying crucially on the interplay between electron correlations and band topology. |
|
 Junkai Dong Harvard University  |
Phonons in Electron Crystals with Berry CurvatureRecent advances in 2D materials featuring nonzero Berry curvature have inspired extensions of the Wigner crystallization paradigm. Recently, the anomalous Hall crystal (AHC) was proposed as another class of electron crystal with nonzero Chern number, inspired by recent experiments in rhombohedral graphene. This poster concerns the low-energy effective theory for such quantum crystals. We first discuss scenarios in which the crystals host one or two gapless phonon modes, which resembles the finite field or zero field Wigner crystals. We also identify a previously overlooked `kineo-elastic’ term in the phonon effective action that is present in the symmetry setting of rhombohedral graphene, and leads to dramatic differences in phonon speeds in opposite directions. We finally discuss models in which the AHC can exhibit transitions in lattice geometry, signaled through an instability in the phonon theory.
|
|
 Joseph Eix Iowa State University  |
Anisotropic SU(4) Kondo ScreeningWe explore the possibility of anisotropic Kondo screening in generic J=3/2 Kondo and Anderson impurity models with tetragonal crystal fields, using a combination of poor man’s scaling and numerical renormalization group (NRG). With these techniques, we can examine the anisotropic screening of the magnetic and orbital susceptibilities at different temperatures and in different model regimes. Notably, we can explore the crossover between SU(4) and SU(2) Kondo physics, which at higher temperatures appears to be mainly driven by anisotropic hybridization rather than the crystal field itself. Our analysis helps establish a correspondence between anisotropic Kondo couplings and experimentally observed temperature scales while developing a better understanding of data obtained from numerical simulations. |
|
 Peleg Emanuel Weizmann Institute of Science  |
A Unifying Framework for Fractional Chern Insulator StabilizationWe present a theory of fractional Chern insulator stabilization against charge-ordered states. We argue that the phase competition is captured by an effective interaction range, which depends on both the bare interaction range and quantum geometric properties. We claim that short effective interaction ranges stabilize fractional states while longer-range interactions favor charge-ordered states. To confirm our hypothesis, we conduct a numerical study of the generalized Hofstadter model using the density matrix renormalization group. Our theory offers a new interpretation of the geometric stability hypothesis and generalizes it, providing a unifying framework for several approaches to fractional phase stabilization. Finally, we propose a route towards experimental verification of the theory and possible implications for fractional states in bands with higher Chern numbers. |
|
 Erin Fleck Stanford University  |
Probing spin-orbit interactions near a topological phase transition using spin-ARPESAngle-resolved photoemission spectroscopy (ARPES) is a powerful technique that enables the direct measurement of electronic band structure. Spin-resolved ARPES in addition directly probes the spin polarization of photoemitted electrons, providing deeper insight into the underlying physics of these materials, though the intrinsic inefficiency of spin detection has proven to be a significant barrier to harnessing the full power of this technique. Recent progress in creating increasingly efficient methods of spin detection have thus stimulated a wealth of spin-ARPES measurements across a wide range of materials. Leveraging the increasing capability of this technique, we have performed high-resolution spin-ARPES measurements to observe the spin texture of a material on the threshold of a topological phase transition, ZrTe5. Our work reveals spin-polarized electronic bands as the material approaches a topological phase transition and offers new perspectives on how spin-orbit interactions manifest in the topological character of this material. We highlight strong light polarization dependence of the spin texture, which further evidences coupling between the spin and orbital degrees of freedom. Beyond the material of study, our results underscore the growing capabilities of spin-resolved ARPES and its potential to uncover novel spin-dependent phenomena in complex materials. |
|
 Rafael Alvaro Flores Calderon Max Planck Institute for the Physics of Complex Systems  |
Unconventional Spin Dynamics and Supersolid Excitations in the Triangular-Lattice XXZ ModelMotivated by recent experiments, we investigate the spin-1/2 XXZ model on the triangular lattice with strong Ising anisotropy, combining large-scale numerical simulations and analytical methods to uncover unconventional spin dynamics. First, we compute the dynamical spin structure factor using density matrix renormalization group (DMRG) simulations and find excellent agreement with inelastic neutron scattering data on the layered compound K2Co(SeO3)2. The low-energy spectrum reveals a roton-like minimum at the M point—absent in linear spin-wave theory—accompanied by peak intensity and a broad continuum above it. Near the Γ point, we observe an approximately linear dispersion with vanishing spectral weight. Second, we compare two analytical frameworks that reproduce the observed features. The first is a hard-core boson approach, which includes: (i) an effective staggered boson model (ESBM) at zero magnetic field, (ii) perturbation theory applied to the one-third magnetization plateau, and (iii) a self-consistent mean-field Schwinger boson theory (SBT). The second framework is based on a variational supersolid quantum dimer model (QDM) ansatz, combined with a single-mode approximation. The SBT captures the broad continuum, the M-point minimum, and linear dispersion at Γ, whereas the QDM reproduces the roton minimum and linear dispersion at finite momentum near Γ. Remarkably, both the QDM wavefunction and the DMRG ground state exhibit nearly identical structure factors with pronounced transverse photon-like excitations. Together, our comprehensive theoretical and numerical analysis elucidates the microscopic origin of supersolid excitations in the XXZ triangular lattice model and their proximity to a spin liquid phase observed experimentally. |
|
 Anna Grigoreva University of Washington  |
Axion electrodynamics and giant magnetic birefringence in Weyl excitonic insulatorsWe show that in the excitonic insulator phase of time-reversal (TR) invariant Weyl semimetals (WSMs), the phase of the exciton condensate couples to the electromagnetic (EM) field as a massive dynamical axion. This is a consequence of the chiral anomaly and the chiral magnetic effect in the parent WSM. The mass of the axion is generated by the inter-band matrix elements of electron-electron interactions and is much smaller than the gap in the single-particle spectrum. Because of this, in the presence of magnetic field the axion coupling to EM fields results in giant anisotropic polarizability and birefringence. The photon-axion hybridization produces a magneto-induced polariton resonance near the axion gap. |
|
 Haoyu Guo Cornell University  |
Phonon induced Energy Relaxation in Quantum Critical MetalsMetals near electronic quantum phase transitions show unusual charge transport, competing orders, and hightemperature superconductivity—hallmarks of non-Fermi liquid behavior. A ubiquitous experimental observation is the emergence of a universal timescale that governs electrical transport and momentum relaxation. An equally important but underexplored question is how energy from electronic excitations relaxes to the environment. We develop a universal theory for energy relaxation in a marginal Fermi liquid, mediated by acoustic phonons. The theory predicts temperature-dependent crossovers governed by emergent energy scales. Our results provide a framework for interpreting recent nonlinear optical measurements in hole-doped cuprates. |
|
 Andrew Hardy University of Toronto 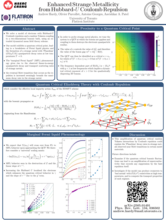 |
Enhanced Strange Metallicity due to Hubbard-U Coulomb RepulsionWe solve a model of electrons with Hubbard-Coulomb repulsion and a random Yukawa coupling to a two-dimensional bosonic bath, using an extended dynamical mean field theory scheme. Our model exhibits a quantum critical point, at which the repulsive component of the electron interactions strongly enhances the effects of the quantum critical bosonic fluctuations on the electrons, leading to a breakdown of Fermi liquid physics and the formation of a strange metal with “Planckian” quasiparticle decay rates at low temperatures (T → 0) . Furthermore, the eventual Mott transition that occurs as the repulsion is increased seemingly bounds the maximum decay rate in the strange metal. Our results provide insight into low-temperature strange metallicity observed in proximity to a Mott transition, as is observed, for instance, in recent experiments on certain moiré materials. |
|
 Mohammad Hassan Caltech  |
A second harmonic generation study of the ACuTe2O7 quasi-1D materialsQuasi-one-dimensional polar materials can potentially exhibit interesting properties such as pronounced non-linear optical responses like second harmonic generation and optical rectification. A comparative study of optical second harmonic generation from BaCuTe2O7, which is polar, and SrCuTe2O7, which is reportedly non-polar and centrosymmetric will be presented here. The relationship between the SHG magnitude and the onset of magnetic correlations in these compounds will also be shown. |
|
 Kazi Ranjibul Islam University of Minnesota  |
Unconventional superconductivity near a nematic instability in a multi-orbital systemWe analyze superconductivity in a multi-orbital fermionic system near the onset of a nematic order, using doped FeSe as an example. We associate the nematic order with spontaneous polarization between dzx and dyz orbitals. We derive the pairing interaction, mediated by soft nematic fluctuations, and show that it is attractive, and that its strength depends on the position on the Fermi surface. As the consequence, right at the nematic quantum-critical point (QCP), superconducting gap opens up at Tc only at special points and extends into finite arcs at T < Tc. In between the arcs the Fermi surface remains intact. This gives rise to highly unconventional behavior of the specific heat, with no jump at Tc and an apparent finite offset at T = 0, when extrapolated from a finite T. We argue that this behavior is consistent with the specific heat data for FeSe1-xSx near critical x for the onset of a nematic order. We discuss the behavior of the gap away from a QCP and the pairing symmetry, and apply the results to FeSe1-xSx and FeSe1-xTex , which both show superconducting behavior near the QCP distinct from that in a pure FeSe. We also computed variation of the specific heat with a magnetic field, magnetic susceptibility, density of states, tunneling conductance, Raman intensity, superfluid stiffness and penetration depth without and with impurity scattering and for the latter computed also optical conductivity and Tc variation. We find good agreement with the existing data for FeSe1-xSx and FeSe1-xTex and suggest new experiments. |
|
 Andrew Ivanov Caltech |
New rigorous insights into scars in PXP-type systemsBy applying specially developed numerical techniques, we uncover previously unknown highly non-trivial exact zero-energy eigenstates hidden within the zero-energy manifolds of the non-integrable PXP-type models parametrized by the Rydberg blockade radius. We derive sufficient conditions for any matrix product state to represent an exact zero-energy eigenstate of a given one-dimensional kinetically constrained model and use them to prove the new eigenstates. Our results highlight a previously unrecognized structure characteristic of the exponentially large nullspaces in kinetically constrained models, suggesting the possibly of extensively many increasingly complex area-law zero-energy eigenstates in the thermodynamic limit. The profound implications of these emergent exact eigenstates for the general thermalization phenomenology are exemplified by one of the states introduced in this work, which is demonstrated to be a member of the primary Z2 quantum many-body scar tower. |
|
 Zheting Jin Yale University  |
First principle prediction of structural distortions in the cuprates and their impact on electronic structureDescribing the normal state of doped cuprates remains a challenge due to strong electronic correlations and structural complexity. While many-body methods have provided deep insights into the correlation effect, they often rely on simplified Hamiltonians that overlook key structural effects. Here, we demonstrate how density functional theory (DFT) can accurately capture essential structural, electronic, and magnetic properties of a prototype cuprate Bi2Sr2CaCu2O8+x (Bi-2212), and how the structural effects refine effective models. By incorporating energy-lowering structural distortions with state-of-the-art exchange-correlation functionals, our DFT calculations achieve the following: (a) an accurate description of the insulating antiferromagnetic ground state in the undoped compound; (b) prediction of the lowest-energy hole-doped crystal structure consistent with scanning transmission electron microscopy; (c) identification of nearly degenerate competing spin and charge stripe orders in the hole-overdoped regime, indicating strong spin fluctuations; and (d) revealing the structural origin of shadow Fermi surface observed in angle-resolved photoemission spectroscopy (ARPES) measurements. Additionally, we show that capturing dynamic spin fluctuations through a many-body approach is essential for quantitatively reproducing ARPES spectra in overdoped cuprates, exposing the severe limitations of band theory methods such as DFT in this context. Finally, we show that the local structure of the CuO2 layers, rather than dopant electrostatic effects, modulates the local charge-transfer gaps, local correlation strengths, and by extension the local superconducting gaps. Reference: Zheting Jin and Sohrab Ismail-Beigi, Phys. Rev. X 14, 041053 (2024). |
|
 Sandeep Joy Florida State University |
||
 Wilhelm Kadow Technical University of Munich  |
From Bose-Fermi Mixtures to Kinetic Magnetism in Moiré HeterostructuresMoiré heterostructures are fascinating experimental platforms for studying emergent quantum many-body phenomena. Here, we realize an equilibrium Bose-Fermi mixture in a bilayer electron system implemented in a WS2/WSe2 moiré heterobilayer with strong Coulomb coupling to a nearby moiré-free WSe2 monolayer. Absent the fermionic component, the underlying bosonic phase manifests as a dipolar excitonic insulator. By injecting excess charges into it, we show that the bosonic phase forms a stable mixture with added electrons but abruptly collapses upon hole doping. We develop a microscopic model to explain the unusual asymmetric stability. Moreover, a similar setup can realize an approximate SU(4)-symmetric Hubbard model. Using matrix product states, we theoretically investigate the magnetic order upon hole doping, where several competing states emerge due to kinetic magnetism. |
|
 Jaewon Kim University of California at Berkeley  |
Linear Magnetoresistance from Glassy OrderSeveral strongly correlated metals display B-linear magnetoresistance (LMR) with a universal slope, in sharp contrast to the quadratic scaling predicted by Fermi liquid theory. We provide a unifying explanation of the origin of LMR by focusing on a common feature in their phase diagrams – proximity to symmetry-breaking orders. Specifically, we demonstrate via two microscopic models that LMR with a universal slope arises ubiquitously near ordered phases, provided the order parameter either (i) has a finite wave-vector, or (ii) has nodes on the Fermi surface. We elucidate the distinct physical mechanisms at play in these two scenarios, and derive upper and lower bounds on the field range for which LMR is observed. Finally, we discuss possible extensions of our picture to strange metal physics at higher temperatures, and argue that our theory provides an understanding of recent experimental results on thin film cuprates and moiré materials.
|
|
 Luke Kim MIT  |
Topological Chiral Superconductivity in Flat Band MaterialsWe propose a beyond-BCS mechanism for superconductivity, inspired by the recently observed chiral superconductivity in rhombohedral graphene system. We derive the topological order and the conductance properties of these new types of superconductors. To see that this can be manifest at suitable densities, we perform variational Monte Carlo calculations on both the chiral superconductor ansatz and the Fermi liquid at general dispersion of combining quadratic and quartic dispersions.
|
|
 Sunghoon Kim Cornell University  |
Correlated Insulators, Superconductors, and Quantum Criticality in Moiré MaterialsMoiré transition metal dichalcogenide (TMD) materials provide a versatile platform for studying the interplay of strong correlations, disorder, and band topology in a highly tunable setting. In this poster, I will present my recent works that describe the role of topology, disorder, and quantum criticality on the experimental phenomenology of TMD bilayers. These include a theoretical explanation for the nontrivial electrical transport near a bandwidth-tuned metal-insulator transition in AA-stacked MoTe₂/WSe₂ [1], an investigation of the interaction-driven insulating phases at a commensurate filling in AB-stacked MoTe₂/WSe₂ [2], and a proposal for the continuous superconductor-insulator transition at a filling of one electron per moire unit cell in twisted bilayer WSe₂ [3]. [1] SK, Senthil, and Chowdhury, Phys. Rev. Lett. 130, 066301 (2023) |
|
 Emmanouil Kokkinis University of Minnesota  |
Pseudogap in electron doped cuprates: thermal precursor to magnetismWe study pseudogap behavior in a metal near an antiferromagnetic instability and apply the results to electron-doped cuprates. We associate pseudogap behavior with thermal magnetic fluctuations and compute the fermionic self-energy along the Fermi surface beyond Eliashberg approximation. We analyze the spectral function as a function of frequency (energy distribution curves, EDC) and momentum (momentum distribution curves, MDC). We show that the EDC display pseudogap behavior with peaks at a finite frequency at all momenta. On the other hand, MDC peaks disperse within the pseudogap, ending at a gossamer Fermi surface. We analyze magnetically-mediated superconductivity and show that thermal fluctuations almost cancel out in the gap equation, even when the self-energy is obtained beyond the Eliashberg approximation. We favorably compare our results with recent ARPES study [K-J Xu et al, Nat. Phys. 19, 1834–1840 (2023)] |
|
 Will Liang Johns Hopkins University 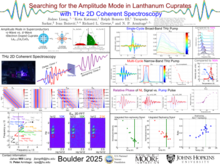 |
Investigating Amplitude Mode in Lanthanum Cuprates Using THz 2D Coherent SpectroscopySignatures of the amplitude mode has been reported in various conventional and unconventional superconductors. Many of these recent studies utilize optical techniques to probe the non-linear response of these systems, but most of them find it challenging to distinguish the response of the amplitude mode from that of quasi-particle excitations and other processes. Recently, THz 2D coherent spectroscopy has been shown to be uniquely sensitive to the amplitude mode in an s-wave superconductor NbN. Our study adapts this method to probe the presence of amplitude mode in electron-doped and hole-doped lanthanum cuprates. Utilizing controlled high-intensity broad-band and narrow-band THz pulses, we find the coherent 2D NL response from lanthanum class cuprates to be significantly different from that of conventional superconductors and attribute this mainly to the over-damping of the amplitude mode and the anisotropic d-wave superconducting gap. |
|
 Jesse Liebman Johns Hopkins University  |
Exploring Electronic Ferroelectricity in BEDT-TTF based Organic Mott InsulatorsThe organic Mott insulators of the form κ-(BEDT-TTF)2X, where BEDT-TTF refers to bis(ethylenedithio)tetrathiafuvalene and X refers to a polyatomic anion, host a correlated electron system on a triangular lattice of (BEDT-TTF)2 dimers. Each dimer lattice site carries one hole and one S=1/2 spin which interacts antiferromagnetically between neighboring dimer lattice sites. Long range charge correlations between dimer lattice sites compete with intradimer hopping, leading to a charge degree of freedom and emergent electric dipoles within (BEDT-TTF)2 dimers. The interplay of strong antiferromagnetic interactions with Ising-like electric dipoles yields a rich phase diagram with quantum spin liquid candidates, quantum dipole liquid candidates, electronic ferroelectricity, and superconductivity. We use Raman scattering spectroscopy to study the insulating regions of the phase diagram, exploring the behavior of emergent electric dipoles with and without long range charge order. We examine the relationship between emergent electric dipoles with a quantum spin liquid candidate, revealing a coupling between the lattice, charge, and spin at lowest temperatures. We use uniaxial strain to tune interactions between (BEDT-TTF)2 dimers, which leads to an experimental mapping of the charge order phase boundary. Lastly, we calculate the electron-molecular-vibration coupling induced shifts to molecular vibrations, which leads to an experimental determination of the extended Hubbard model parameters that is unique. We find that exotic and disordered ground states emerge from the competition between intradimer and interdimer interactions, the coupling of multiple degrees of freedom, and the broad range of frequencies which correspond to dipole and spin fluctuations. |
|
 Nandagopal Manoj Caltech  |
Non-commutative effective field theory of the lowest Landau level superfluidA 2+1D superfluid in a rapidly rotating trap forms an array of vortices, with collective excitations called Tkachenko modes. Du et al. (2024) argued from an effective field theory viewpoint that these excitations are described by a field theory living on a non-commutative space. We elucidate the microscopic origin of these non-commutative fields, and present a novel derivation of the effective field theory for this superfluid using a lowest Landau level projected coherent state path integral approach. Besides conceptual clarity, this approach makes quantitative predictions about the long-wavelength, low-energy behavior in terms of the microscopic parameters of the weakly interacting lowest Landau level superfluid – relevant to trapped Bose-Einstein condensate experiments. |
|
 Anqi Mu Columbia University |
Effects of collective modes on nonlinear conductivity |
|
 Matthew O'Brien University of Illinois Urbana-Champaign  |
Quantum dynamics of 2D randomly pinned charge density wavesThe nature of dynamic charge correlations in randomly pinned charge density waves (CDW) is a long-standing theoretical problem. The inherent disorder present in real materials and the particular fragility of charge order to impurities makes this problem especially relevant to a host of systems currently at the forefront of modern condensed matter physics, including the cuprate high temperature superconductors and transition metal dichalcogenides. To address this question, we build on an exactly-solvable model of a 2D randomly pinned incommensurate CDW first introduced by us, and use the large-N technique to determine the phase diagram and CDW correlations. Our approach considers quantum and thermal fluctuations and disorder on equal footing by treating all effects non-perturbatively. We reveal a novel crossover between under-damped and over-damped dynamics of the fluctuations of the CDW order. |
|
 Yugo Onishi Massachusetts Institute of Technology  |
Universal bounds in topological phasesTopology plays a fundamental role in condensed matter physics. Even when ground states share the same symmetries, they can still be topologically distinct, giving rise to distinct topological phases of matter. These phases are characterized by topological invariants, such as the Chern number. Topological invariants can manifest in physical observables, such as the quantized Hall conductance in Chern insulators. In this work, we explore another fundamental aspect of topological phases: the existence of universal bounds on physical observables, which we term topological bounds. Specifically, we establish bounds on two physical observables in Chern insulators: the static structure factor and the energy gap. The bound on the static structure factor is determined solely by the Chern number, while the bound on the energy gap is determined by the Chern number and the electron density. Remarkably, these bounds apply universally to all insulators, including strongly correlated systems such as fractional Chern insulators. As an example, we apply these bounds to moiré transition metal dichalcogenides. We also interpret the topological bounds as geometric relations with quantum geometry. Our results provide a new perspective on topological phases of matter, demonstrating that the topological invariants can universally manifest as topological bounds. [1] Y. Onishi and L. Fu, Topological Bound on the Structure Factor, Phys. Rev. Lett. 133, 206602 (2024).
[2] Y. Onishi and L. Fu, Fundamental Bound on Topological Gap, Phys. Rev. X 14, 011052 (2024). |
|
 Grgur Palle University of Illinois Urbana-Champaign  |
Consistent Treatment of Multiple Vestigial Orders within Saddle-Point ApproximationsWhen a primary order breaks multiple symmetries, partially ordered phases, known as vestigial phases, may arise which breaks only some of them at a higher temperature. Yet for a given primary order, there are generically multiple possible vestigial orders, each one described by a composite order parameter (OP) that is quadratic in the multi-component OP of the primary order. Which vestigial order prevails is dictated by the quartic self-interactions of the primary OP. However, within saddle-point analyses of this problem, there is a large ambiguity in the results. Because the different vestigial channels feed into each other, as specified by the Fierz identities, one can apparently enhance or eliminate altogether the condensation tendency in any vestigial channel. Here, we resolve this ambiguity. By carefully introducing a large-N limit which respects both the initial group structure and the Fierz identities, we deduce a unique prescription for how the saddle-point approximation (SPA) must be carried out. Compared to previous SPA, we find non-trivial competition between the different vestigial channels, as specified by the symmetrized quartic coefficients. In addition, we establish agreement of our SPA to mean-field variational and self-consistent Hartree-Fock approximations at weak coupling. We illustrate our prescription on three examples: X-point charge-density waves in primitive tetragonal systems, M-point spin-density waves in hexagonal systems, and multi-component superconductivity in cubic systems. |
|
 Akshat Pandey Stanford University |
||
 Emile Pangburn Paris-Saclay University  |
Topological charge excitations and Green's function zeros in paramagnetic Mott insulatorWe investigate the emergence of topological features in the charge excitations of Mott insulators in the Chern-Hubbard model. In the strong correlation regime, treating electrons as the sum of holons and doublons excitations, we compute the topological phase diagram of Mott insulators at half-filling using composite operator formalism. The Green function zeros manifest as the tightly bound pairs of such elementary excitations of the Mott insulators. Our analysis examines the winding number associated with the occupied Hubbard bands and the band of Green’s function zeros. We show that both the poles and zeros show gapless states and zeros, respectively, in line with bulk-boundary correspondence. The gapless edge states emerge in a junction geometry connecting a topological Mott band insulator and a topological Mott zeros phase. These include an edge electronic state that carries a charge and a charge-neutral gapless zero mode. Our study is relevant to several twisted materials with flat bands where interactions play a dominant role. |
|
 Aaditya Panigrahi Rutgers University  |
Spontaneous Pair Density Wave in a Fractionalized Kondo LatticeWe demonstrate that the discommensuration between the Fermi surfaces of a conduction sea and an underlying spin liquid provides a natural mechanism for the spontaneous formation of pair density waves. Using a recent formulation of the Kondo lattice model which incorporates a Yao Lee spin liquid proposed by the authors, we demonstrate that doping away from half-filling induces finite-momentum electron-Majorana pair condensation, resulting in amplitude-modulated PDWs. Our approach provides a precise, analytically tractable pathway for understanding the spontaneous formation of PDWs in higher dimensions and offers a natural mechanism for PDW formation in the absence of Zeeman splitting, and naturally accounts for the emergence of intertwined order. |
|
 Archisman Panigrahi MIT  |
Fermion Statistics Induced Spin Chirality and Young's Interference Patterns of Spin Chirality in Topological SuperconductorsWe demonstrate that in both normal and superconducting metals with broken time-reversal symmetry (TRS), orbital currents in the ground state can induce spin-chirality. Remarkably, non-zero chirality can emerge purely due to Fermion statistics, without the need for spin-dependent interactions, even when the ground state remains spin-unpolarized. This chirality in the carrier band generates a chiral three-spin RKKY interaction between localized spins coupled to the carriers via the s-d Hamiltonian, an effect detectable by local probes like spin-sensitive STM. The spatial distribution of chirality exhibits Young’s interference patterns near localized magnetic adatoms. The interference arises because Bogoliubov quasiparticles are coherent superposition of electrons and holes with opposite spins, allowing coherent and reversible particle-to-hole conversion within the superconductor bulk. Magnetic adatoms act as beam splitters, enabling interference between particle and hole states, leading to spatial patterns similar to those observed in Young’s double-slit experiment. In topological superconductors, these interference patterns are further modulated by nodal lines that encode the winding numbers of the superconducting gap function’s phase. In systems such as topological superconductors where detecting TRS breaking by conventional means is challenging, local detection of spin chirality provides a reliable diagnostic of superconducting topological phases and also provides insight about the nature of pairing. |
|
 Alireza Parhizkar University of Maryland  |
Zero Flux Localization: How flat bands magically appearI present a very simple and clear answer to the question of why the chiral limit of the bilayer graphene clicks and gives flat bands at specific twist angles. The solution is simple enough to be given as homework in a grad course. |
|
 Taka Park University of California Santa Barbara / Princeton |
||
 Marvin Qi University of Chicago  |
Bound on the emergence of hydrodynamicsLate-time, long-wavelength dynamics of generic many-body interacting quantum systems at finite temperature are described by hydrodynamics. The timescale of the onset of hydrodynamics is naturally interpreted as a local thermalization time. It is natural to expect that thermalization occurs faster when interactions are stronger. We prove that thermalization cannot occur arbitrarily quickly: hydrodynamics can only emerge after a “Planckian” timescale τeq ≥ β ℏ. |
|
 Aidan Reddy MIT |
||
 Felipe Reyes-Osorio University of Delaware  |
Nonequilibrium field theory of open spin systems: from semiclassical to nonperturbative quantum dynamicsOpen systems of many interacting spins—as realized by localized magnetic moments in a spintronic device, or qubits in a quantum computer—pose a formidable challenge for presently available theoretical methods, especially when the memory effects induced by the surrounding environment are relevant. Even archetypical examples like the spin-boson model, in which a single spin interacts with a continuum of bosonic modes requires switching between specialized methods for different choice of system-bath parameters. Here, we present a field theory (FT) of open quantum spin systems based on the Schwinger-Keldysh (SK) functional integral, which serves as the starting point for both semiclassical and fully quantum descriptions of the dynamics. In the semiclassical regime, we obtain corrections to the Landau-Lifshitz-Gilbert equations, conventionally employed in spintronics and magnonics, accounting for, e.g., nonlocal magnetic damping. On the other hand, the fully quantum regime is probed by combining SKFT with the two-particle irreducible (2PI) action resumming a class of Feynman diagrams to an infinite order. Remarkably, our SKFT+2PI closely tracks numerically exact benchmarks for the spin-boson and spin-chain-boson models, even in the nonperturbative and non-Markovian regime. The favorable numerical cost of solving integro-differential equations produced by SKFT+2PI framework with increasing number of spins, time steps or spatial dimensionality makes it a promising route for simulation of driven-dissipative systems in quantum computing or quantum spintronics and magnonics in the presence of a single or multiple dissipative environments. |
|
 Benjamin Sappler Technical University of Munich  |
Diagonal isometric form for tensor product states in two dimensionsIsometric tensor product states (isoTPS) generalize the isometric form of the one-dimensional matrix product states (MPS) to tensor networks in two and higher dimensions. Here, we introduce an alternative isometric form for isoTPS by incorporating auxiliary tensors to represent the orthogonality hypersurface. We implement the time evolving block decimation (TEBD) algorithm on this new isometric form and benchmark the method by computing ground states and the real time evolution of the transverse field Ising model in two dimensions on large square lattices of up to 1250 sites. Our results demonstrate that isoTPS can efficiently capture the entanglement structure of two-dimensional area law states. The short-time dynamics is also accurately reproduced even at the critical point. Our isoTPS formulation further allows for a natural extension to different lattice geometries, such as the honeycomb or kagome latice.
|
|
 Tixuan Tan Stanford University  |
Origin or interaction-induced Chern band in rhombohedral multilayer grapheneWe propose an ansatz wavefunction for describing the interaction- induced Chern 1 band in rhombohedral graphene, or in any holomorphic parent band.
|
|
 Konstantinos Vasiliou University of Oxford  |
Electrons interacting with Goldstone modes: The rotating frameIn an electronic system with Spontaneous Symmetry Breaking (SSB), the low-energy spectrum contains gapless Goldstone modes. How do these Goldstone modes interact with the electrons? In the long wavelength limit, the electrons are expected to decouple from the Goldstone modes in analogy with the case of phonons. If so, the dominant scattering processes are expected to be with zone-boundary modes. This approach develops a generic framework to understand this problem for any continuous SSB phase and sheds light on some non-trivial modifications to the theory to recover the expected behavior of the scattering vertex, as well as its implications on the resulting spectral functions. |
|
 Maria Visscher Max Planck Institute for Chemical Physics |
Designed cleaving planes in ruthenium dioxide for ARPES experimentsRuthenium dioxide has a complex band structure, underpinning a variety of phenomena including superconductivity under strain and a Dirac nodal line network. It has also been proposed as a candidate altermagnet, and although recent studies suggest it lacks the requisite magnetic order, it has been shown to host unusual spin-polarised states in its band structure. These phenomena motivate the need for further studies into its electronic structure. Angle-resolved photoemission spectroscopy (ARPES) would be an ideal probe for this, and while there have been several pioneering studies to date, the three-dimensional structure of ruthenium dioxide makes it difficult to prepare the requisite clean and flat surfaces with conventional methods. We have therefore investigated a fabrication method based on Focused Ion Beam (FIB) structuring to stimulate sample cleavage along desired crystallographic planes. With this method, we were able to obtain high quality surfaces, on which we performed ARPES measurements. This capability to tailor the sample cleavage leads to a significant increase in ARPES data quality, allowing new resolution of subtle band splitting and additional resolution of bulk vs. surface states in this system. |
|
 Yaar Vituri Weizmann Institute of Science |
||
 Cristian Voinea University of Leeds  |
Regularizing 3D conformal field theories via anyons on the fuzzy sphereIn the recently introduced “fuzzy sphere” method, numerical regularization of certain 3D conformal field theories (CFTs) is achieved through the non-commutative geometry of the lowest Landau level filled by electrons; here, the charge is trivially gapped due to the Pauli exclusion principle at filling factor v=1, while the electron spins encode the desired CFT. Successful applications of the fuzzy sphere to paradigmatic CFTs, such as the 3D Ising model, raise an important question: how finely tuned does the underlying electron system need to be? In this work, we will show that the 3D Ising CFT can also be realized at fractional electron fillings, unaffected by the exchange statistics of the particles or the nature of topological order in the charge sector. In such cases, the CFT spectrum is intertwined with the charge-neutral spectrum of the underlying fractional quantum Hall (FQH) state – a feature that is trivially absent in the previously studied v=1 case. Remarkably, the mixing between the CFT and the FQH spectra is strongly suppressed within the numerically-accessible system sizes. |
|
 Xuepeng Wang Cornell University  |
Intertwined Orders, Spin-Polarons and Exotic Quantum Criticality in Correlated Topological Flat BandsWe consider a sign-problem-free, time-reversal symmetric model with isolated Chern bands, involving both spin and valley degrees of freedom in the presence of a class of repulsive electronic interactions. We analyze the phase diagram using a numerically exact quantum Monte Carlo (QMC) method. We find intertwined orders between a Chern antiferromagnet and a spin-singlet superconductor. The superconductivity is mediated by Cooper pairs formed from spin-polarons/skyrmions and is robust against a weak spin-orbit coupling field. We analyze the possibility of approximate emergent symmetry and exotic quantum critical points. The low-temperature phase diagram can be understood in terms of a superspin nonlinear sigma model. |
|
 Yiming Wang Rice University  |
Shot noise in strongly correlated metalsThe nature of charge carriers in strange metals is a subject of considerable interest. Recent measurements in the quantum-critical heavy-fermion metal YbRh2Si2 motivate an investigation of shot noise across various models. We first establish that F=√3/4 is a universal property of all Fermi liquids, analogous to the Wiedemann-Franz law. This result underscores the absence of quasiparticles in YbRh2Si2 . Next, we examine shot noise in a system of electrons coupled to critical bosons and demonstrate the emergence of electron-boson drag, which equalizes the local temperatures of both components. Results at the Kondo-destruction quantum critical point will also be presented. |
|
 Ziwei Wang University of Oxford |
A Closed Band-Projected Density Algebra Must be Girvin-MacDonald-PlatzmanThe band-projected density operators in a Landau level obey the Girvin-MacDonald-Platzman (GMP) algebra, and a large amount of effort in the study of fractional Chern insulators has been directed towards approximating this algebra in a Chern band. In this paper, we prove that the GMP algebra, up to form factors, is the only closed algebra that projected density operators can satisfy in two and three dimensions, highlighting the central place it occupies in the study of Chern bands in general. A number of interesting corollaries follow. |
|
 Josephine Yu Stanford University 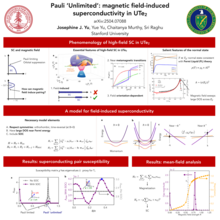 |
Pauli 'unlimited': magnetic field induced-superconductivity in UTe2Inspired by the observation of extreme field-boosted superconductivity in uranium ditelluride, we present a scenario in which superconductivity can be induced by a strong Zeeman field, rather than destroyed by it, as is the case in Pauli-limited superconductivity. The resulting superconducting state has an upper critical field far greater than the superconducting transition temperature, and with spin-orbit coupling, it is sensitive to the field orientation. We demonstrate the interplay between superconductivity and metamagnetism in a simple effective theory. |
|
 Jia-Xin Zhang University of California Santa Barbara |
Identifying Instabilities with Quantum Geometry in Flat Band SystemsFlat-band systems lack a well-defined Fermi surface, challenging the conventional nesting-based picture of instabilities toward Landau order. We introduce generalized Bloch vectors to reveal an intrinsic nesting structure encoded in the band geometry, leading to maximal susceptibility at the mean-field level and driving ordered phases. We further show that the correlation length of an order parameter satisfying perfect nesting—even at finite momentum—is entirely characterized by a generalized quantum metric, and is therefore lower-bounded in topologically non-trivial bands. As an example, we demonstrate hidden nesting for staggered antiferromagnetic spin order in an exactly flat-band model—contrary to the usual association of flat bands with ferromagnetism. Determinantal quantum Monte Carlo confirms the emergence of this long-range order. We further show that breaking time-reversal symmetry can induce an FFLO-like state without Zeeman splitting. |
|
 Xinghai Zhang Rice University  |
Universal wave function statistics and superconductivity in quasiperiodic twisted trilayer grapheneTwisted multilayer graphene (TMG) was recently discovered to host superconductivity and offers a much richer playground to study moiré physics, with more knobs to tune including multiple twist angles. The low-energy physics of TMG is described by multi-cone Dirac fermions coupled with matrix-value fields, which are effectively topological when inter-valley scattering is suppressed. The topology protection prevents the wave functions from being Anderson (or Wannier) localized by quasiperiodicity; the latter is natural in TMG with 3 or more layers due to inevitable interlayer twist-angle differences. Here we focus on quasiperiodic twisted trilayer graphene (TTG). We employ two different models, with and without a collinear approximation for the moiré wavevectors [1]. We show that quasiperiodic TTG behaves like a dirty surface of a bulk class-AIII topological insulator, and exhibits “spectrum-wide quantum criticality” [2] that is robust in the absence of exotic surface-coupling scenarios [3]. We show that superconductivity can be enhanced without fine-tuning to magic angles, similar to previous results in a model of quasiperiodic TBLG [4]. We also explore how the chiral symmetry breaking terms affects the wave function statistics and superconductivity. [1] Ziyan Zhu, Stephen Carr, Daniel Massatt, Mitchell Luskin, and Efthimios Kaxiras, PRL 125, 116404 (2020) |
|
 Yunchao Zhang MIT  |
Phase Transitions between Obstructed Atomic InsulatorsI will present critical theories that describe the phase transitions between different types of trivial atomic insulators. |
|
 Boran Zhou Johns Hopkins University  |
Ancilla theory and its application in twisted bilayer grapheneThe recent experimental studies of twisted bilayer graphene (TBG) raise a fundamental question: how do we understand Mott localization in a topological band? In this work, we offer a new perspective of Mott physics, which can be generalized to TBG directly in momentum space. In our theory, the Mott gap is understood as from an exciton-like hybridization Φ(k)c^\dagger(k)ψ(k) between the physical electron c and an ancilla fermion ψ. In the conventional Mott insulator of trivial band, the hybridization is s-wave with Φ(k) = U/2, where U is the on-site Hubbard interaction. On the other hand, the band topology in TBG enforces a topological Mott hybridization with Φ(k)~kx ± iky in a small region around k = 0. We dub this new Mott state as topological Mott localization because of the p±ip order parameter analogous to the topological superconductor. At ν = 0, we find a topological Mott semimetal with a low energy effective theory resembling that of the untwisted bilayer graphene. For ν = ±1,±2,±3, we show transitions from correlated insulators to Mott semimetals at smaller U. In the most intriguing density region ν = −2−x, we propose a symmetric pseudogap metal at small x, which hosts a small Fermi surface and violates the perturbative Luttinger theorem. Interestingly, the quasiparticle is primarily formed by ancilla fermion, which we interpret as a composite fermion formed by a hole bound to a particle-hole pair. Our theory offers a unified language to describe the Mott localization in both trivial and topological bands in momentum space, and we anticipate applications in other moir´e systems with topological Wannier obstruction, such as the twisted transition-metal dichalcogenide (TMD) homobilayer.
|
|
 Bo Zou University of Texas, Austin  |
Vortices and vortex lattices in the bilayer exciton superfluids in the quantum Hall regimeIn bilayer systems doped with electrons and holes separately, interlayer excitons are formed by Coulomb attraction and condense in low temperatures. This superfluid phase persists in high magnetic fields and competes with the quantum Hall phase in each layer without inter-layer coherence. The vortex excitations have fractionalized electric charge and will form a honeycomb lattice in a small concentration when the electrons and holes are doped slightly imbalanced. |
|
 Dmitry Zverevich University of Wisconsin-Madison |
Magnetism of the Bilayer Wigner CrystalThe multiple-spin exchange frequencies of the bilayer Wigner crystal are determined by the semiclassical method, which is asymptotically exact in the limit of dilute electron densities. The evolution of the exchange frequencies with interlayer distance - as the crystal undergoes a sequence of structural transitions - leads to both ferromagnetic and multi-sublattice antiferromagnetic phases. Extrapolation of the results to higher density suggests a rich magnetic phase diagram of the bilayer Wigner crystal, including the possibility of spin-nematic and valence-bond solid phases. The bilayer crystal is stable to higher electron densities than the monolayer, leading to enhanced magnetic energy scales. Our estimates of the exchange energies suggest some of the magnetic phases may be accessible in recently discovered bilayer Wigner crystals in a transition-metal dichalcogenide system. |

