Student Poster Abstracts
Please note that while there is not one required or mandatory size, all posters should fit in a space no longer than 36” (91 cm) wide and preferably be no more than about 48” (122 cm) in height. Arrangements can be made for other sizes as necessary.
If you are not able to get your poster printed before you leave home (or are unable to easily transport), you may get posters printed at FedEx Office (http://local.fedex.com/co/boulder/office-0402/).
 Maryam Abbasi Washington University in St. Louis  |
Topological Quantum State Control In The Presence Of An Exceptional PointIn this poster, I will present our research on the quantum behavior of a non-Hermitian qubit constructed by a dissipative superconducting transmon circuit. By tuning the system parameters in real-time to encircle an exceptional point, we achieve nonreciprocal quantum state transfer and explore topological features of the complex energy landscape. Alternatively, we can employ a dilation procedure involving an ancillary qubit to simulate the evolution under non-Hermitian Hamiltonians using unitary gates, which can allow us to explore more interesting features of these systems. |
|
 Suchita Agrawal Max Planck Institute of Quantum Optics, Germany  |
Realizing and probing programmable 2D optical lattices with flexible geometries and connectivityOver the past decade, ultracold atoms in optical lattices have become a vital platform for experimental quantum simulation, enabling precise studies of a variety of quantum many-body problems. For most experiments, the layout of the confining lattice beams restricts the accessible lattice configurations and thus the underlying physics. Here, we present a novel tunable lattice, which provides programmable unit cell connectivity and in principle allows for changing the geometry mid-sequence. Our approach builds on the generation of phase-stable realisation of a square or triangular base lattice combined with microscopically projected repulsive local potential patterns. With this technique, we realise Lieb and Kagome lattices, and benchmark the various configurations by exploring single particle quantum walks. We explore many body physics in these lattices by observing parity fluctuations associated with the superfluid-to-Mott insulator transition. As an outlook, we will explore how the presented lattices can be applied for spin-selective imaging as well as doublon detection. |
|
 Sajant Anand University of California, Berkeley  |
Holographic Quantum State Preparation of Isometric Tensor NetworksWhile standard approaches to quantum simulation require a number of qubits proportional to the number of simulated particles, current noisy quantum computers are limited to tens of qubits. With the technique of holographic quantum simulation, a D-dimensional system can be simulated with a D−1-dimensional subset of qubits, enabling the study of systems significantly larger than current quantum computers. Using circuits derived from the multiscale entanglement renormalization ansatz (MERA), we accurately prepare the ground state of an L=32 critical, non-integrable perturbed Ising model and measure long-range correlations on the 10 qubit Quantinuum trapped ion computer. We introduce generalized MERA (gMERA) networks that interpolate between MERA and matrix product state networks and demonstrate that gMERA can capture far longer correlations than a MERA with the same number of qubits, at the expense of greater circuit depth. Finally, we comment on extensions to time evolution and higher dimensions. |
|
 Shankar Balasubramanian MIT |
Quantum computation from dynamic automorphism codesWe propose a new model of quantum computation comprised of low-weight measurement sequences that simultaneously encode logical information, enable error correction, and apply logical gates. These measurement sequences constitute a new class of quantum error- correcting codes generalizing Floquet codes, which we call dynamic automorphism (DA) codes. We construct an explicit example, the DA color code, which is assembled from short measurement sequences that can realize all 72 automorphisms of the 2D color code. On a stack of N triangular patches, the DA color code encodes N logical qubits and can implement the full logical Clifford group by a sequence of two- and, more rarely, three-qubit Pauli measurements. We also make the first step towards universal quantum computation with DA codes by introducing a 3D DA color code and showing that a non-Clifford logical gate can be realized by adaptive two-qubit measurements. |
|
 Mircea Bejan University of Cambridge  |
Measurement-induced Simulability Phase TransitionClassical simulations of quantum systems are conjectured to be generically hard. The amount of entanglement in the system relates to the complexity of classical simulation, therefore, the measurement-induced phase transitions in entanglement suggest a phase transition in the classical simulability of quantum systems. Entanglement, however, is not fully equivalent to complexity since, for example, Clifford circuits can generate entanglement while being efficient to classically simulate. In this poster, I will describe how measurement-induced phase transitions relate to classical simulability, taking Clifford circuits as the starting point. |
|
 Silvia Cardenas Lopez Columbia University  |
Many-Body Superradiance and Dynamical Mirror Symmetry Breaking in Waveguide QEDThe many-body decay of extended collections of two-level systems remains an open problem. Here, we investigate whether an array of emitters coupled to a one-dimensional bath undergoes Dicke superradiance. This is a process whereby a completely inverted system becomes correlated via dissipation, leading to the release of all the energy in the form of a rapid photon burst. We derive the minimal conditions for the burst to happen as a function of the number of emitters, the chirality of the waveguide, and the single-emitter optical depth, both for ordered and disordered ensembles. Many-body superradiance occurs because the initial fluctuation that triggers the emission is amplified throughout the decay process. In one-dimensional baths, this avalanchelike behavior leads to a spontaneous mirror symmetry breaking, with large shot-to-shot fluctuations in the number of photons emitted to the left and right. Superradiant bursts may thus be a smoking gun for the generation of correlated photon states of exotic quantum statistics. |
|
 Jeremy Côté Université de Sherbrooke 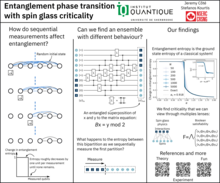 |
Entanglement phase transition with spin glass criticalityWe define an ensemble of random Clifford quantum circuits whose output state undergoes an entanglement phase transition between two volume-law phases as a function of measurement rate. Our setup maps exactly the output state to the ground space of a spin glass model. We identify the entanglement phases using an order parameter that is accessible on a quantum chip. We locate the transition point and evaluate a critical exponent, revealing spin glass criticality. Our work establishes an exact statistical mechanics theory of an entanglement phase transition. |
|
 Tyler Ellison Yale University  |
Floquet codes with a twistFloquet codes are a novel class of dynamical quantum error-correcting codes, whose ability to encode quantum information emerges from a periodic schedule of non-commuting measurements. Early examples of Floquet codes offer a promising alternative to the well-established surface code, since they exhibit relatively high error thresholds and can be efficiently implemented using only two-body measurements. In this work, we describe a new means for storing and processing quantum information in Floquet codes by introducing point-like twist defects. We focus on an example in which the dynamics possess an anomalous 1-form symmetry, which allows us to create twist defects by gauging the 1-form symmetry along a spatial path. Importantly, our construction maintains the connectivity of the lattice, preserves the period of the measurement schedule, and requires only two-body measurements. We also discuss how the notion of higher gauging can also be used to construct Floquet codes characterized by the topological order of certain Abelian twisted quantum doubles. |
|
 Ali Fahimniya University of Maryland  |
Hyperbolic Floquet Quantum Error Correcting CodesLarge-scale universal quantum computation requires protecting quantum information against quantum noise which can be performed using quantum error-correcting codes. Recently, Hastings and Haah [1] introduced a fault-tolerant dynamical subsystem code on a honeycomb lattice using two-qubit check measurements. Despite having zero logical qubits when viewed as a static subsystem code, the sequence of two-qubit measurements protects two dynamical logical qubits. On the other hand, hyperbolic surface codes are known as a generalization of toric code on a negatively curved manifold. Since the genus of such manifolds increases with the system size, it has been demonstrated that these codes possess a constant encoding rate. In this work, we introduce hyperbolic Floquet codes, where two-qubit check operators are measured in a periodic sequence. Using this measurement scheme, first, we show that the number of dynamically protected logical qubits grows with the system size. Next, we numerically demonstrate the existence of a threshold for the error rate of physical qubits that our code can protect against. [1] Hastings, M. B., and Jeongwan H., “Dynamically generated logical qubits” Quantum 5 (2021): 564. |
|
 Shi Feng The Ohio State University  |
Anyon response in field-driven quantum spin liquidsWhether the fractionalized excitations, such as those that emerge from Kitaev’s honeycomb model, have sharp signatures that can be detected in experiments? We show that while the response to single spin excitations is broad, the spectral function corresponding to two-spin excitations across a bond in the Abelian spin liquid phase has sharp signatures that can be attributed to specific anyons even at the linear response regime. Driven by a magnetic field, the composite gauge fermion therein disperses along a specific one-dimensional direction that provides a fingerprint of fractionalization. At lower anistropy in the center of the Abelian phase, the field generates a hybridization between the gauge fermion and the majorana fermion, resulting in a different one-dimensional dispersion pattern. These highly constrained fracton-like dispersions can be observable by inelastic light and neutron scattering, thereby providing “smoking gun” signatures of fractionalization in the Abelian QSL phase. We also discuss the deconfined spinon in the intermediate-field-driven phase of the Kitaev model, which harbors a neutral gapless spinon Fermi surface. By using a data-centric quantum-classical hybrid machine learning approach that characterizes complex quantum many-body states using interpretable classical machine learning, we demonstrate spinon Friedel oscillation at momenta 2kF potentially measurable in magnetic scattering or STM experiments. |
|
 Xiaozhou Feng The Ohio State University  |
Measurement-induced phase transitions on dynamical quantum treesMonitored many-body systems fall broadly into two dynamical phases, “entangling” or “disentangling”, separated by a transition as a function of the rate at which measurements are made on the system. Producing an analytical theory of this measurement-induced transition is an outstanding challenge. Recent work made progress in the context of tree tensor networks, which can be related to all-to-all quantum circuit dynamics with forced (postselected) measurement outcomes. So far, however, there are no exact solutions for dynamics of spin-1/2 degrees of freedom (qubits) with “real” measurements, whose outcome probabilities are sampled according to the Born rule. Here we define dynamical processes for qubits, with real measurements, that have a tree-like spacetime interaction graph, either collapsing or expanding the system as a function of time. The former case yields an exactly solvable measurement transition. We explore these processes analytically and numerically, exploiting the recursive structure of the tree. We compare the case of “real” measurements with the case of “forced” measurements. Both cases show a transition at a nontrivial value of the measurement strength, with the real measurement case exhibiting a smaller entangling phase. Both exhibit exponential scaling of the entanglement near the transition, but they differ in the value of a critical exponent. An intriguing difference between the two cases is that the real measurement case lies at the boundary between two distinct types of critical scaling. On the basis of our results we propose a protocol for realizing a measurement phase transition experimentally via an expansion process. |
|
 Shachar Fraenkel Tel Aviv University  |
Extensive long-range entanglement in a nonequilibrium steady stateEntanglement measures constitute powerful tools in the quantitative description of quantum many-body systems out of equilibrium. We analytically study entanglement in the steady state of noninteracting fermions, occupying a one-dimensional lattice that hosts a generic scatterer at its center and is coupled at its ends to two biased reservoirs. We show that disjoint intervals located on opposite sides of the scatterer, and within similar distances from it, maintain volume-law entanglement regardless of their separation, as measured by their fermionic negativity. The mutual information of the intervals, which quantifies the total correlations between them, follows a similar scaling. We find that this behavior arises whenever the occupation functions of the two reservoirs differ, thus capturing both the case of a chemical-potential bias and the case of a temperature bias (as well as any combination of the two). By deriving exact expressions for the extensive terms of the negativity and mutual information, we prove their simple and universal functional dependence on the scattering probabilities associated with the scatterer. This simple dependence allows to demonstrate that the strong long-range entanglement is generated by the coherence between the transmitted and reflected parts of propagating particles within the energy window of the bias. This contribution is based on arXiv:2205.12991, as well as on newer results. |
|
 Haoyang Gao Harvard University  |
Robust qudit Hamiltonian engineering and dynamical decoupling from graphical constructionsHamiltonian engineering and dynamical decoupling has been an important tool in quantum sensing, NMR, and quantum many-body physics for decades. Despite extensive research on this topic, this technique is still limited in spin-1/2 systems. In this poster, we propose a new method for doing robust Hamiltonian engineering and dynamical decoupling in general qudit systems, enabling the exploration of novel many-body phenomena that are inaccessible in spin-1/2 case, and the possibility to do better quantum sensing utilizing the larger dipole moment of higher-spin particles. As an example of showing the power of our method, we designed a robust disorder and interaction decoupling sequence for our experimental platform of interacting nitrogen-vacancy (NV) centers (spin-1 particles), and realized experimentally an order of magnitude improvement in coherence time compared with previous sequences. As an unrelated work, I will also talk about our recent effort of engineering one-axis twisting (OAT) and two-axis-twisting (TAT) dynamics in a solid state (NV) spin ensemble, which is useful in realizing spin squeezing and another closely related (but different) interaction enhanced metrology method that we call “spin amplification”. |
|
 Hyunsoo Ha Princeton University  |
Many-Body Resonances in the Avalanche Instability of Many-Body LocalizationMany-body localized (MBL) systems fail to reach thermal equilibrium under their own dynamics, even though they are interacting, nonintegrable, and in an extensively excited state. One instability toward thermalization of MBL systems is the so-called “avalanche,” where a locally thermalizing rare region is able to spread thermalization through the full system. The spreading of the avalanche may be modeled and numerically studied in finite one-dimensional MBL systems by weakly coupling an infinite-temperature bath to one end of the system. We find that the avalanche spreads primarily via strong many-body resonances between rare near-resonant eigenstates of the closed system. Thus we find and explore a detailed connection between many-body resonances and avalanches in MBL systems. |
|
 Ahmed Hajr University of California, Berkeley  |
2D Kerr-Cat Qubit: Experimental Realization and Technical ChallengesThe Kerr Cat qubit is a bosonic qubit with autonomous protection from bit flips and serves as a promising candidate for implementing quantum error correction codes tailored for noise-biased qubits. However, the first realizations of this qubit were hosted in 3D cavities with either small cat size limited by heating effects or small nonlinearities leading to slow gates. In this work, we demonstrate improved coherence with stabilized cat states in 2D chips by using the SNAIL (Superconducting Nonlinear Asymmetric Inductive eLement) and implementing single qubit gates in 150ns on average. We identify heating effects from the stabilization drive as the limiting factor for the lifetime of the coherent states and outline how to reduce the heating effects and improve the intrinsic decay rate of the bare oscillator by making design changes. |
|
 Stav Haldar Louisiana State University  |
Measurement-induced phase transitions in the Sachdev-Ye-Kitaev modelContinuous monitoring of an otherwise closed quantum system has been found to lead to a measurement-induced phase transition (MIPT) characterized by abrupt changes in the entanglement or purity of the many-body quantum state. For an entanglement MIPT, entangling dynamics compete with measurement dynamics, pushing the system either to a phase with extensive entanglement or to a phase with low-level entanglement. For purification MIPTs, projective measurements effectively cool and localize the system, inducing a transition from a mixed state to an uncorrelated pure state. In this work, we numerically simulate monitored dynamics in the all-to-all Sachdev-Ye-Kitaev (SYK) model for finite N. We witness both entanglement and purification MIPTs in the steady-state. It is often said that there is an equivalence between entanglement and purification MIPTs, however we provide numerical evidence to the contrary, implying that entanglement and purification MIPTs are indeed two distinct phenomena. The reason for such a distinction is quite simple: entanglement can revive after a completely projective measurement – if measurements do not occur too often in time – but impurity cannot. |
|
 Jacob Hauser University of California, Santa Barbara  |
Continuous symmetry breaking in adaptive quantum dynamicsAdaptive quantum circuits, in which unitary operations, measurements, and feedback are used to steer quantum many-body systems, provide an exciting opportunity to generate new dynamical steady states. We introduce an adaptive quantum dynamics with continuous symmetry where unitary operations, measurements, and local unitary feedback are used to drive ordering. In this setting, we find a pure steady state hosting symmetry-breaking order, which is the ground state of a gapless, local Hamiltonian. We explore the dynamical properties of the approach to this steady state. We find that this steady-state order is fragile to perturbations, even those that respect the continuous symmetry. |
|
 Sumner Hearth Boston University  |
Unitary k-designs from random number-conserving quantum circuitsLocal random circuits scramble efficiently and accordingly have a range of applications in quantum information and quantum dynamics. With a global U(1) charge however, the scrambling ability is reduced; for example, such random circuits do not generate the entire group of number-conserving unitaries. We show that finite moments cannot distinguish the ensemble that local random circuits generate from the Haar ensemble on the entire group of number-conserving unitaries. Specifically, the circuits form a kc-design with kc = O(Ld) for a system in d spatial dimensions with linear dimension L. For k < kc, the depth τ to converge to a k-design scales as τ \gtrsim k Ld+2. In contrast, without number conservation τ \gtrsim k Ld. The convergence of the circuit ensemble is controlled by the low-energy properties of a frustration-free quantum statistical model which spontaneously breaks k U(1) symmetries. The associated Goldstone modes are gapless and lead to the predicted scaling of τ. Our variational bounds hold for arbitrary spatial and qudit dimensions; we conjecture they are tight. |
|
 Yi Huang University of Minnesota  |
Anderson transition in non-Hermitian disordered systemsWe study the Anderson transition for three-dimensional tightly bound cubic lattices where both real and imaginary parts of on-site energies are independent random variables distributed uniformly between −W/2 and W/2. Such a non-Hermitian analog of the Anderson model is used to describe random-laser medium with local loss and amplification. We employ eigenvalue statistics to search for the Anderson transition. For 25% smallest-modulus complex eigenvalues we find the average ratio r of distances to the first and the second nearest neighbor as a function of W. For a given system size N, the function r(W) crosses from 0.72 to 2/3 with a growing W demonstrating a transition from delocalized to localized states. When plotted at different N all r(W) cross at W = 6.0 ± 0.1 (in units of nearest-neighbor overlap integral) clearly demonstrating the 3D Anderson transition. We find that in the non-Hermitian 2D Anderson model, the transition is replaced by a crossover. |
|
 Joseph Iosue University of Maryland, College Park  |
Page curves and typical entanglement in linear opticsBosonic Gaussian states are a special class of quantum states in an infinite dimensional Hilbert space that are relevant to universal continuous-variable quantum computation as well as to near-term quantum sampling tasks such as Gaussian Boson Sampling. In this work, we study entanglement within a set of squeezed modes that have been evolved by a random linear optical unitary. We first derive formulas that are asymptotically exact in the number of modes for the Rényi-2 Page curve (the average Rényi-2 entropy of a subsystem of a pure bosonic Gaussian state) and the corresponding Page correction (the average information of the subsystem) in certain squeezing regimes. We then prove various results on the typicality of entanglement as measured by the Rényi-2 entropy by studying its variance. Using the aforementioned results for the Rényi-2 entropy, we upper and lower bound the von Neumann entropy Page curve and prove certain regimes of entanglement typicality as measured by the von Neumann entropy. Our main proofs make use of a symmetry property obeyed by the average and the variance of the entropy that dramatically simplifies the averaging over unitaries. In this light, we propose future research directions where this symmetry might also be exploited. We conclude by discussing potential applications of our results and their generalizations to Gaussian Boson Sampling and to illuminating the relationship between entanglement and computational complexity. |
|
 Linta Joseph Dartmouth College  |
Decoupling dipolar interactions in dense spin ensemblesHamiltonian engineering techniques can be used to engineer certain classes of desired Hamiltonians various systems. In solid-state nuclear spin ensembles, such techniques help design pulse sequences that effectively decouple the strong magnetic dipolar interactions that dominate the system Hamiltonian. Although these decoupling sequences were originally designed to narrow spectral lines and improve resolution in NMR spectroscopy, the effective extension of coherence times achieved is also important for quantum control, simulation and sensing applications. In this work, we study the decoupling efficiency of a number of dipolar decoupling sequences with a focus on their sensitivity to experimental imperfections and other possible errors. |
|
 Anish Kulkarni Princeton University  |
Lindbladian dynamics of the Sachdev-Ye-Kitaev modelWe study the open quantum dynamics of the Sachdev-Ye-Kitaev (SYK) model. The SYK system is coupled to a Markovian bath. The dynamics is thus described by the Lindblad master equation. We compute various physical properties in the limit of large number of Majorana fermions. As a probe of the open quantum dynamics, we compute the averaged Loschmidt echo, namely the average overlap between the initial and time-evolved density matrices. The Loschmidt echo reveals first and second-order dynamical phase transitions in the SYK Lindbladian models. We also compute the steady-state Green’s functions and associated decay rates and find an underdamped to overdamped transition. |
|
 Abhishek Kumar University of Massachusetts, Amherst  |
Boundary Transfer Matrix Spectrum of Measurement-Induced TransitionsMeasurement-induced phase transitions are described by non-unitary conformal field theories (CFT) whose precise nature remains unknown. Most physical quantities of interest, such as the entanglement features of quantum trajectories, are described by boundary observables in this CFT. We introduce a boundary transfer matrix approach to study the boundary spectrum of this field theory, and we consider a variety of boundary conditions, including boundary dissipation. We apply this approach numerically to monitored Haar and Clifford circuits, and to the measurement-only Ising model where the boundary scaling dimensions can be derived analytically. |
|
 Ethan Lake MIT  |
Multipole Symmetries in Many-Body PhysicsI will discuss recent work on the many body physics of systems with multipolar conservation laws, in which a total charge and various multipole moments thereof are conserved. Particular focus will be placed on Hubbard models with dipole moment conservation, which enjoy a natural experimental realization in strongly tilted optical lattices. The bosonic versions of these models possess unusual insulating Bose-Einstein condensates and unconventional patterns of spontaneous symmetry breaking, while the fermionic versions host exotic non-Fermi liquids. I will also discuss the ramifications that multipole conservation has for diffusive dynamics, where it leads to unusually large dynamical exponents and exponentially localized steady states. |
|
 Youenn Le Gal Collège de France  |
Non Hermitian physics in free fermions monitored dynamicsWe explore the relevance of non-Hermitian physics in the framework of free fermion dynamics under monitoring. In this context, it has been proposed that similar entanglement behavior could be observed in the effective non-Hermitian Hamiltonian and the corresponding monitored dynamics. In this study, we examine the entanglement in the non-Hermitian SSH model, which exhibits an entanglement transition from volume to area law. Surprisingly, this transition does not coincide with PT-symmetry breaking. We confirm that the entanglement behavior of the monitored SSH model does not match the one of the non-Hermitian problem. Subsequently, we suggest some features that could explain these qualitative differences. |
|
 Su-un Lee University of Chicago  |
Dynamical phase transitions in noisy random circuitsUnderstanding the dynamics of noisy random circuits holds significant theoretical importance and practical relevance. By examining the dynamics of quantum and classical correlations under various error rates, we observe and analyze sharp transitions in both time and error rate. Specifically, the entanglement dynamics exhibit distinct behaviors dependent on the scaling of the error rate in terms of system size N. (1) When the error rate decays faster than 1/N, entanglement rapidly saturates and decreases at a constant rate. (2) When the error rate decays at a rate of 1/N, entanglement gradually increases and then decreases at a constant rate. (3) When the error rate decays slower than 1/N, entanglement accumulates and abruptly disappears thereafter. Remarkably, for all cases, the entanglement vanishes non-analytically at the transition time, marking a sharp boundary between these different dynamical regimes. To investigate these dynamical phase transitions, we introduce the bipartite semiglobal model—a simplified circuit that captures the essential interplay between scrambling and decoherence. Our analysis is further supported by numerical simulations, validating our conclusions. |
|
 Cathy Li University of Pennsylvania 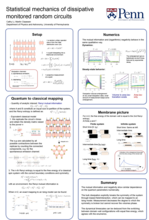 |
Statistical Mechanics of Monitored Dissipative Random CircuitsDissipation is inevitable in realistic quantum circuits. We examine the effects of dissipation on a class of monitored random circuits that exhibit a measurement-induced entanglement phase transition. This transition has previously been understood as an order-to-disorder transition of an effective classical spin model. We extend this mapping to include on-site dissipation described by the dephasing and spontaneous emission channel and study the corresponding 2D Ising model with generalized interactions and develop diagrammatic methods for the exact Boltzmann weights of the bonds in terms of probability of measurement p, the dissipation rate Γ and the on-site Hilbert space dimension q. The dissipation plays the role of Z2-symmetry-breaking interactions, while small measurement rates reduces the ratio of the symmetry-breaking interactions to the pairwise interactions, conducive to long-range order. We analyze the dynamical regimes of the R ́enyi mutual information and find that the joint action of monitored measurements and dissipation yields short time, intermediate time and steady state behavior that can be understood in terms of crossovers between different classical domain wall configurations. The presented analysis applies to monitored open or Lindbladian quantum systems and provides a tool to understand entanglement dynamics in realistic dissipative settings and achievable system sizes. |
|
 Zhu-Xi Luo Harvard University  |
Gapped interfaces in fracton models and foliated fieldsThis work investigates the gapped interfaces of foliated field theories that describe fracton phases of matter, focusing on the X-cube model as an example. We analyze the gapped interfaces between X-cube and the vacuum (gapped boundary), 3+1D toric code, and another X-cube model. The interfaces can be either undecorated or decorated, with the latter involving adding $K$-matrix Chern-Simons type terms to specific undecorated interfaces. We systematically identify the undecorated interfaces for the aforementioned cases and explore general decorations, supported by many examples. We further demonstrate the formulation of lattice models for the general gapped interfaces found in foliated field theories and present several illustrative instances. While previous literature has discussed the gapped boundaries of the X-cube model, our formalism facilitates the straightforward establishment of new decorated boundaries. This work is a collaboration with Po-Shen Hsin and Ananth Malladi. |
|
 Daniel Mark MIT  |
Ancilla-Assisted Shadow Tomography: Measuring Arbitrary Physical Properties in Analog Quantum SimulationI will introduce a protocol for measuring arbitrary observables that can be implemented in today’s analog quantum simulation platforms. A key challenge in analog quantum simulation is to measure desired physical properties. Conventional approaches necessitate a high level of control unavailable to most present-day quantum devices. Our protocol—inspired by “classical shadow tomography”—involves introducing ancillary degrees of freedom to the state of interest, evolving the joint system under native Hamiltonian dynamics, then measuring globally in a single, fixed basis. Information about all observables is contained in the measurement data, which can be extracted using classical data processing. I will numerically demonstrate our approach with examples relevant to neutral atom arrays and quantum gas microscopes, only assuming existing technology. Our protocol promises to overcome limited controllability in analog simulators and thus enhance the versatility and utility of near-term quantum technologies. |
|
 Anne Matthies University of Cologne  |
Programmable adiabatic demagnetization for systems with trivial and topological excitationsPreparing the ground state of a many-body Hamiltonian on a quantum device is of central importance, both for quantum simulations of molecules and materials, and for a variety of quantum information task. Different approaches to ground state preparation have been proposed, including variational quantum simulation, adiabatic evolution and, more recently, also simulated cooling. We propose a simple, robust protocol to prepare a low-energy state of an arbitrary Hamiltonian on a quantum computer. The protocol is inspired by the “adiabatic demagnetization” technique, used to cool solid state systems to extremely low temperatures. The adiabatic cooling protocol is demonstrated via an application to the transverse field Ising model. We use half of the qubits to model the system and the other half as a bath. Each bath spin is coupled to a system spin. In a strong magnetic field, the bath spins are prepared in the polarized ground state. By an adiabatic downward sweep of the magnetic field, we change the energy of the bath spins and allow for resonant processes that transfer entropy from the system to the bath qubits. After each cycle, the bath is reset to the ground state. We find that the performance of the algorithm in the presence of a finite error rate depends on the nature of the excitations of the system; systems with non-local (topological) excitations are more difficult to cool. Finally, we explore ways to partially mitigate this problem. arXiv:2210.17256 |
|
 Saranyo Moitra Tata Institute of Fundamental Research  |
Entanglement Entropy of Interacting Fermions from Correlation functionsEntanglement measures such as entanglement entropy (EE) have been shown to exhibit characteristic scaling behaviour with subsystem size in a variety of novel quantum states. However, analytical methods to calculate EE have been limited to non-interacting theories, or theories with conformal symmetry in one spatial dimension. Numerical methods applicable to more generic interacting systems can access small sizes owing to the exponentially growing complexity of the problem. Adapting recent Wigner-characteristic based techniques, we show that Renyi EE of interacting fermions in arbitrary dimensions can be represented as a Schwinger-Keldysh free energy on replicated manifolds with a current between the replicas. The current is local in real space and is present only in the subsystem of interest. This allows us to construct a diagrammatic representation of EE in terms of connected correlators in the standard unreplicated field theory. We further decompose EE into “particle” contributions which depend on the one-particle correlator, two-particle connected correlator and so on. For repulsively interacting fermions in two and three dimensions, we find the one particle contribution to entanglement picks up a leading volume scaling which is entirely determined by the incoherent piece of the one-particle momentum distribution function. The coefficient of the now subleading log-enhanced area piece is seen to decrease with increasing interaction strength. |
|
 Giacomo Morpurgo University of Geneva 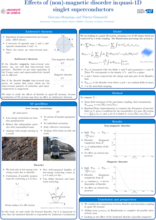 |
Effect of (non)-magnetic disorder in quasi-1D singlet superconductorsWe investigate the effects of the combination of interactions and disorder in a quasi 1D system. In this case, the critical temperature of superconductivity is an interesting observable for this purpose. Anderson’s theorem indeed states that BCS-type superconductivity is resistant to non-magnetic disorder because time- reversal invariance is still preserved. In quasi 1D systems, since there the effect of disorder and interactions is more important than in higher dimensional systems, the Anderson theorem is generally not respected. We here study the competition between disorder and interactions in such systems by considering forward scattering disorder, both for magnetic and non-magnetic impurities. Using a field theory representation and renormalization, we show that non magnetic disorder preserves Tc in agreement with Anderson theorem. However, for the magnetic disorder, we find a reduction of the spin-gap and compute the reduction of Tc. We investigate the consequences for systems made of fermionic tubes with at- tractive interactions. |
|
 Frederik Møller Atominstitut, Vienna University of Technology  |
Emergent hydrodynamics and Pauli blocking in quasi-1D Bose gasesMany-body quantum systems with reduced dimensionality often exhibit properties strikingly different from that of three-dimensional (3D) systems. Confinement of atoms to a single line (1D) leads, for example, to strongly correlated motion of the atoms. The resulting collective excitations are quasi-particles, whose properties may differ significantly from the atoms; in a Bose gas, correlation effects due to interactions in 1D prevent two collective excitations from occupying the same quantum state. This imposed Pauli exclusion leads to effective fermionization of the quantum Bose gas in 1D even for weak interatomic repulsion; similar fermionization in 3D occurs only for extremely strong repulsion. In our experiment we show that these theoretical concepts have far-reaching consequences even in real systems which always are only approximately 1D. We prepare a Bose gas of weakly interacting rubidium atoms under tight transverse confinement on an AtomChip. Next, we perturb the system to initiate dynamics and monitor its relaxation by measuring the atomic density. Tuning the temperature allows us to probe the regime where a non-negligible fraction of atoms have sufficiently high energy to cause transverse excitations. Even in this regime, far beyond conventional limits of 1D, the system relaxes slowly in agreement with 1D physics of effective fermionization of the quantum Bose gas. Our observations represent a manifestation of the emergent Pauli blocking of excitations, whereby our system remains effectively 1D. |
|
 Amirreza Negari Perimeter Institute  |
Measurement-induced phase transition in Toric codeWe show how distinct phases of matter can be generated by performing random single-qubit measurements on a subsystem of toric code. Using a parton construction, such measurements map to random Gaussian tensor networks, and in particular, random Pauli measurements map to a classical loop model in which watermelon correlators precisely determine measurement-induced entanglement. Measuring all but a 1d boundary of qubits realizes hybrid circuits involving unitary gates and projective measurements in 1+1 dimensions. We find that varying the probabilities of different Pauli measurements can drive transitions in the un-measured boundary between phases with different orders and entanglement scaling, corresponding to short and long loop phases in the classical model. Furthermore, by utilizing single-site boundary unitaries conditioned on the bulk measurement outcomes, we generate mixed state ordered phases and transitions that can be experimentally diagnosed via linear observables. This demonstrates how parton constructions provide a natural framework for measurement-based quantum computing setups to produce and manipulate phases of matter. |
|
 Akshat Pandey Stanford University  |
Random geometry at an infinite-randomness fixed pointWe study the low-energy physics of the critical (2+1)-dimensional random transverse-field Ising model. The one-dimensional version of the model is a paradigmatic example of a system governed by an infinite-randomness fixed point, for which many results on the distributions of observables are known via an asymptotically exact renormalization group (RG) approach. In two dimensions, the same RG rules have been implemented numerically, and demonstrate a flow to infinite randomness. However, analytical understanding of the structure of this RG has remained elusive due to the development of geometrical structure in the graph of interacting spins. To understand the character of the fixed point, we consider the RG flow acting on a joint ensemble of graphs and couplings. We propose that the RG effectively occurs in two stages: (1) randomization of the interaction graph until it belongs to a certain ensemble of random triangulations of the plane, and (2) a flow of the distributions of couplings to infinite randomness while the graph ensemble remains invariant. This picture is substantiated by a numerical RG in which one obtains a steady-state graph degree distribution and subsequently infinite-randomness scaling distributions of the couplings. Both of these aspects of the RG flow can be approximately reproduced in simplified analytical models. |
|
 Gunhee Park Caltech  |
Efficient embedding framework for tensor network influence functional of Anderson impurity modelWe develop a quantum embedding theory for constructing a tensor network-based influence functional method in quantum impurity models, such as the Anderson impurity model. Here, we formulate a tensor network method that can project bath degrees of freedom into the embedding bath orbital space. The original discrete-time formalism is extended to the continuous-time formulation, which is expressed by the differential equation of motion in the embedding space. This framework leads to the algorithm that requires only linear computational costs to the number of timesteps with smaller timestep errors. The numerical performance is compared in the quench dynamics of the single impurity Anderson model. |
|
 Benedikt Placke MPI for the Physics of Complex Systems  |
Statistical mechanics mapping for finite rate qLDPC codesIt is well known that the decoding of zero rate stabilizer codes can be mapped onto statistical mechanics models with quenched disorder. Statistical mechanics mappings were first developed for estimating the maximum-likelihood decoding threshold of the toric code under phenomenological noise models (Dennis et al, 2002), They have since been developed for other stabilizer codes and more general noise models (Chubb and Flammia, 2021). Recently, quantum LDPC codes with finite rate have generated much interest because they could significantly reduce the overhead required for quantum error correction. This makes a generalization of the statistical mechanics mappings to this class of codes desirable. Such a generalization is non-trivial because the mapping has to account for the fact that there is an exponential (in the number of physical qubits) number of possible logical errors. In the language of statistical mechanics this implies that they have a non-vanishing contribution to the entropy of the system. This is in contrast to the case of decoding finite-rate codes, where the number of possible logical errors does not scale with the number of physical qubits. We solve this problem for the case of hyperbolic surface codes, which are close cousins of the (euclidean) surface code but have finite rate. In particular, we show that decoding them under independent bit- and phase-flip noise maps onto what we call the “dual random bond Ising model” in hyperbolic space. As an application of the mapping, we compute the maximum likelihood decoding threshold of a range of hyperbolic surface codes under independent bit- and phase-flip noise. |
|
 Andrew Pocklington University of Chicago  |
Non-Equilibrium Steady States of Driven-Dissipative Lattice Models: Exact Solutions, Topological Light, and Interaction Induced StabilityThe intersection of many-body quantum systems with open dynamics can lead to a number of diverse phenomena that do not appear in their closed counterpart. Specifically in this poster, we begin by looking at a few examples of reservoir engineering – the process by which we can couple a quantum system to a structured (Markovian) bath that deterministically relaxes the quantum system into a nontrivial steady state. We study a non-integrable open spin chain whose steady state is a so-called rainbow state, as well as a way to use correlated dissipation to selectively excite topological edge modes in a photonic lattice. In addition to this, we study ways one can systematically add Hamiltonian interactions to a dynamically unstable photonic lattice to cut off an instability, leading to surprising phenomena like topological lasing as well as the dissipative stabilization of highly non-classical states of light. |
|
 Klée Pollock Iowa State University  |
Variational Microcanonical EstimatorWe propose a variational quantum algorithm for estimating microcanonical expectation values in models obeying the eigenstate thermalization hypothesis. Using a relaxed criterion for convergence of the variational optimization loop, the algorithm generates weakly entangled superpositions of eigenstates at a given target energy density. An ensemble of these variational states is then used to estimate microcanonical averages of local operators, with an error whose dominant contribution decreases as a power law in the size of the ensemble. We apply the algorithm to the one-dimensional mixed-field Ising model, where it converges for ansatz circuits of depth roughly linear in system size. The most accurate thermal estimates are produced for intermediate energy densities and for local operators that appear in the Hamiltonian. In our error analysis, we find connections with recent works investigating the underpinnings of the eigenstate thermalization hypothesis. In particular, the failure of energy-basis matrix elements of local operators to behave as independent random variables is a potential source of error that the algorithm can overcome by averaging over an ensemble of variational states. |
|
 Michael Rampp Max Planck Institute for the Physics of Complex Systems  |
Hayden-Preskill recovery in chaotic and integrable unitary-circuit dynamicsQuantum many-body systems distribute localized information over many non-local degrees of freedom in the course of their time evolution, a process called information scrambling. Information scrambling is related to fundamental questions in quantum dynamics such as thermalization, quantum chaos, and entanglement spreading, and to the control of information dynamics in quantum computing platforms. The Hayden-Preskill protocol probes the capability of information recovery from local subsystems after unitary transformations. It has mostly been discussed for global unitary transformations in the thermodynamic limit without any internal time or length scales. Here, we investigate the use of Hayden-Preskill recovery as a dynamical probe of scrambling in local quantum many-body systems. We present exact results for certain classes of unitary circuit models, both structured (dual-unitary) and Haar-random circuits, and discuss different dynamical signatures corresponding to information transport or scrambling, respectively. Surprisingly, certain chaotic circuits can transport information with perfect fidelity. In integrable dual-unitary circuits, we relate the information transmission to the transport and scattering of quasiparticles. Using numerical and analytical insights, we argue that the qualitative features of information recovery extend away from these solvable points. Our results suggest that information recovery protocols can serve to distinguish chaotic and integrable behavior, and that they can be used to identify characteristic dynamical features, such as quasiparticles or underlying dual-unitarity. |
|
 Vikram Ravindranath Boston College  |
Absorbing Phases in Adaptive CircuitsThis poster discusses the construction of specific target states in 1D quantum circuits using measurements followed by outcome-dependent feedback. There is a critical rate of measurement above which these protocols can be successful, but symmetries can impact their viability. By studying two families of models - qubits undergoing unitary evolution with a special structure, and free fermions - a Z2 symmetry is found to slow the preparation of such states. This is explained by a mapping to Branching-Annihilating Random Walks. |
|
 Jonathon Riddell University of Nottingham  |
Chaos in perturbed dual unitary modelsDual unitary models have been proven to follow quantum chaotic dynamics. In this work, we investigate if the chaotic properties of a wide class of dual unitary models are stable under perturbations away from the dual unitary point. |
|
 Wesley Roberts Northeastern University  |
Fidelity of the Kitaev honeycomb model under a quenchMotivated by rapid developments in the field of quantum computing and the increasingly diverse nature of qubits, we theoretically study the influence that quenched outside disturbances have in an intermediately long time limit. We consider localized imperfections, uniform fields, noise, and couplings to an environment which we study in a unified framework using a prototypical but idealized interacting quantum device - the Kitaev honeycomb model. Our study focuses on the quantum state robustness in response to an outside magnetic field, a magnetic bath, magnetic noise, magnetic impurities, and a noisy impurity. As indicators for quantum robustness, we use the Uhlmann fidelty of the ground state and excited spinon states after a quench. We find that the time dependence of the fidelity often depends crucially on whether the system is gapped. We find that in the gapped case the fidelity decays to a constant value under noiseless quenches, while in a gapless system it exhibits algebraic decay. In all other situations studied, such as coupling to a bath and noisy quenches, both gapped and gapless systems exhibit a universal form for the long-time fidelity, Ce−αtt−β, where the values of C, α, and β depend on physical parameters such as system size, disturbance strength, etc. Therefore, our work provides estimates for the intermediate-long time stability of a quantum device and it suggests under what conditions there appear the hallmarks of an orthogonality catastrophe in the time-dependence of the fidelity. Our work provides engineering guidelines for quantum devices in quench design and system size. |
|
 Sibaram Ruidas Indian Institute of Science |
Classical limit of measurement-induced transition in many-body chaos in integrable and non-integrable oscillator chainsWe discuss the dynamics of integrable and non-integrable chains of coupled oscillators under continuous weak position measurements in the semiclassical limit. We show that, in this limit, the dynamics is described by a standard stochastic Langevin equation, and a measurement-induced transition appears as a noise- and dissipation-induced chaotic-to- non-chaotic transition akin to stochastic synchronization. In the non-integrable chain of anharmonically coupled oscillators, we show that the temporal growth and the ballistic light-cone spread of a classical out-of-time correlator characterized by the Lyapunov exponent and the butterfly velocity are halted above a noise or below an interaction strength. The Lyapunov exponent and the butterfly velocity both act like order parameters, vanishing in the non-chaotic phase. In addition, the butterfly velocity exhibits a critical finite-size scaling. For the integrable model, we consider the classical Toda chain and show that the Lyapunov exponent changes non-monotonically with the noise strength, vanishing at the zero noise limit and above a critical noise, with a maximum at an intermediate noise strength. The butterfly velocity in the Toda chain shows a singular behavior approaching the integrable limit of zero noise strength. |
|
 Subhayan Sahu Perimeter Institute  |
Phase transitions in sampling and error correction in local Brownian circuitsWe study the emergence of anticoncentration and approximate unitary design behavior in local Brownian circuits. The dynamics of circuit averaged moments of the probability distribution and entropies of the output state can be represented as imaginary time evolution with an effective local Hamiltonian in the replica space. This facilitates large scale numerical simulation of the dynamics in 1+1d of such circuit-averaged quantities using tensor network tools, as well as identifying the various regimes of the Brownian circuit as distinct thermodynamic phases. In particular, we identify the emergence of anticoncentration as a sharp transition in the collision probability at log N timescale, where N is the number of qubits. We also show that a specific classical approximation algorithm has a computational hardness transition at the same timescale. In the presence of noise, we show there is a noise-induced first order phase transition in the linear cross entropy benchmark when the noise rate is scaled down as 1/N. At longer times, the Brownian circuits approximate a unitary 2-design in O(N) time. We directly probe the feasibility of quantum error correction by such circuits, and identify a first order transition at O(N) timescales. The scaling behaviors for all these phase transitions are obtained from the large scale numerics, and corroborated by analyzing the spectrum of the effective replica Hamiltonian. |
|
 Konstantinos Sfairopoulos University of Nottingham  |
Boundary conditions dependence of the phase transition in the quantum Newman-Moore modelWe study the triangular plaquette model (TPM, also known as the Newman-Moore model) in the presence of a transverse magnetic field on a lattice with periodic boundaries in both spatial dimensions. We consider specifically the approach to the ground state phase transition of this quantum TPM (QTPM, or quantum Newman-Moore model) as a function of the system size and type of boundary conditions. Using cellular automata methods, we obtain a full characterization of the minimum energy configurations of the TPM for arbitrary tori sizes. For the QTPM, we use these cycle patterns to obtain the symmetries of the model, which we argue determine its quantum phase transition: we find it to be a first-order phase transition, with the addition of spontaneous symmetry breaking for system sizes which have degenerate classical ground states. For sizes accessible to numerics, we also find that this classification is consistent with exact diagonalization, Matrix Product States and Quantum Monte Carlo simulations |
|
 Nanako Shitara University of Colorado, Boulder  |
Noise Spectroscopy Without Dynamical Decoupling PulsesSpectral characterization of noise environments that lead to the decoherence of qubits is critical to developing robust quantum technologies. While dynamical decoupling offers one of the most successful approaches to characterize noise spectra, it necessitates applying large sequences of π pulses that increase the complexity and cost of the method. In this talk, I will introduce a noise spectroscopy method that utilizes only the Fourier transform of free induction decay measurements, thus removing the need for the application any π pulses. This method faithfully recovers the correct noise spectra and outperforms previous dynamical decoupling schemes while significantly reducing its experimental overhead. I will also discuss the experimental feasibility of our proposal and demonstrate its robustness in the presence of statistical measurement noise. Our method is applicable to a wide range of quantum platforms and provides a simpler path toward a more accurate spectral characterization of quantum devices, thus offering possibilities for tailored decoherence mitigation. |
|
 Hansveer Singh University of Massachusetts, Amherst  |
Tunable superdiffusion in integrable spin chain using correlated initial statesAlthough integrable spin chains only host ballistically propagating particles they can still feature diffusive spin transport. This diffusive spin transport originates from quasiparticle charge fluctua- tions inherited from the initial state’s magnetization Gaussian fluctuations. We show that ensembles of initial states with quasi-long range correlations lead to superdiffusive spin transport with a tun- able dynamical exponent. We substantiate our prediction with numerical simulations and explain how deviations arise from finite time and finite size effects. |
|
 Adithya Sriram Stanford University  |
Topology, criticality, and dynamically generated qubits in a stochastic measurement-only Kitaev modelWe consider a paradigmatic solvable model of topological order in two dimensions, Kitaev’s honeycomb Hamiltonian, and turn it into a measurement-only dynamics consisting of stochastic measurements of two-qubit bond operators. We find an entanglement phase diagram that resembles that of the Hamiltonian problem in some ways, while being qualitatively different in others. When one type of bond is dominantly measured, we find area-law entangled phases that protect two topological qubits (on a torus) for a time exponential in system size. This generalizes the recently-proposed idea of Floquet codes, where logical qubits are dynamically generated by a time-periodic measurement schedule, to a stochastic setting. When all types of bonds are measured with comparable frequency, we find a critical phase with a logarithmic violation of the area-law, which sharply distinguishes it from its Hamiltonian counterpart. The critical phase has the same set of topological qubits, as diagnosed by the tripartite mutual information, but protects them only for a time polynomial in system size. Furthermore, we observe an unusual behavior for the dynamical purification of mixed states, characterized at late times by the dynamical exponent z=1/2 – a super-ballistic dynamics made possible by measurements. |
|
 Charles Stahl University of Colorado  |
Robust Ergodicity Breaking in Quantum Loop ModelsI will present a quantum loop model which provably exhibits topologically stable ergodicity breaking. The results follow from a one-form symmetry, which can be exact or emergent. In the latter case, the ergodicity breaking becomes an exponentially long-lived prethermal phenomenon. The model has nonlocal conserved quantities that correspond to a pattern of system-spanning domain walls, and which are robust to the addition of arbitrary k-local perturbations. |
|
 Philippe Suchsland Max Planck Institute for the Physics of Complex Systems  |
Out-of-time-ordered correlators and domain wall relocalisation in transverse field Ising chainsWe study order parameters and out-of-time-ordered correlators (OTOCs) for a wide variety of quantum transverse field Ising chains: thermal and quenched, clean and disordered, integrable and generic. We find a remarkably rich phenomenology, ranging from stable periodic to signals decaying with varying rates. This variety is due to a complex interplay of dynamical constraints which thermalisation is subject to. In particular, a process we term dynamical domain wall relocalisation provides a long-lived signal in the clean, integrable case, which can be degraded by the addition of disorder even without interactions. Our results shed light on the behaviour of OTOC in presence of long lived quasi-particles. |
|
 Spenser Talkington University of Pennsylvania  |
Linear and Non-Linear Optics of Lindbladian SystemsNon-equilibrium quantum systems can exhibit fundamentally different qualitative behavior than their equilibrium counterparts. Here we leverage Keldysh Green’s functions to develop a linear and non-linear response formalism to probe the properties of open quantum systems subject to dissipative evolution by Lindbladian superoperators. We present results for fermionic systems and place a specific emphasis on optical conductivity and the example of Bernal bilayer graphene. Contrary to Hermitian systems: (1) the diamagnetic response may be real and exceptional points manifest themselves in the k-resolved diamagnetic response, (2) the paramagnetic response has a similar magnitude to the equilibrium system but does not manifest universal Dirac behavior, and (3) asymmetric dissipation can enable a second order response in a centrosymmetric system. |
|
 Nathanan Tantivasadakarn Caltech  |
Creation of Non-Abelian Topological Order and Anyons on a Trapped-Ion ProcessorNon-Abelian topological order (TO) is a coveted state of matter that despite extensive efforts has remained elusive. We present the first unambiguous realization of non-Abelian TO and demonstrate control of its anyons. We create the ground state wavefunction of D₄ TO on a kagome lattice of 27 qubits using an adaptive circuit on Quantinuum’s H2 trapped-ion quantum processor. |
|
 Matthew Thibodeau University of Illinois, Urbana-Champaign  |
Preparing ground states of nearly-frustration-free modelsSolving for quantum ground states is important for understanding the properties of quantum many-body systems, and quantum computers are potentially well-suited for solving for quantum ground states. The complexity of this problem has been thoroughly investigated, and the worst-case runtime scaling is known: in particular, it depends inversely on the spectral gap of the Hamiltonian of interest. On the other hand, for the special case of frustration-free Hamiltonians, the scaling relaxes to an inverse square-root dependence. In this work we determine the exact details of how that scaling interpolates between the two cases, by considering the ground state preparation problem restricted to a special subset of Hamiltonians which we term “nearly-frustration-free.” For this subclass, we describe an algorithm whose dependence on the gap is asymptotically better than the worst-case upper bound, and prove that this new dependence is the best achievable up to logarithmic factors. In addition, we give examples of physically motivated Hamiltonians which live in this subclass. Finally, we describe an extension of this method which allows the preparation of excited states both for generic Hamiltonians as well as, at a similar speedup as the ground state case, for those which are nearly frustration-free. |
|
 Julian Thoenniss University of Geneva  |
An efficient method for quantum impurity problems via matrix-product states in the temporal domainWe introduce an efficient method to simulate dynamics of an interacting quantum impurity coupled to non-interacting fermionic reservoirs. Viewing the impurity as an open quantum system, we describe the reservoirs by their Feynman-Vernon influence functionals (IF). The IF are represented as matrix-product states in the temporal domain, which enables an efficient computation of dynamics for arbitrary interactions. We apply our method to study quantum quenches and transport in an Anderson impurity model, including highly non-equilibrium setups, and find favorable performance compared to state-of-the-art methods. The computational resources required for an accurate computation of dynamics scale polynomially with evolution time, indicating that a broad class of out-of-equilibrium quantum impurity problems are efficiently solvable. |
|
 Iris Ulčakar Jožef Stefan Institute, Slovenia  |
Iterative construction of most necessary conserved quantitiesGeneral Gibbs ensembles (GGEs) have been proposed as a local steady state description of integrable many-body systems after a quantum quench. Similarly, GGEs also approximately describe the non-equilibrium steady states of integrable systems weakly coupled to non-equilibrium Markovian baths. We present an iterative method for the latter case, constructing the most necessary conserved quantities for an efficient truncated GGE description. Guided by the integrability-breaking perturbations, the space of conserved quantities is spanned by the action of the baths’ super-operators. |
|
 Carlo Vanoni SISSA - International School for Advanced Studies  |
Interface dynamics in the 2D quantum Ising modelWe consider the non-equilibrium dynamics of the 2d quantum Ising model in the regime of strong ferromagnetic coupling. We study the dynamics of domain walls separating regions of reversed spin orientation. For many initial configurations, we are able to map the problem to a fermionic chain, and show that at leading order there is an emergent integrability. The particular case of a large corner is investigated in details and we then discuss how integrability is broken when the ferromagnetic coupling is large but finite. We show that a symmetry-breaking longitudinal field gives rise to a robust ergodicity breaking in two dimensions, a phenomenon underpinned by Stark many-body localization of the emergent fermionic excitations of the interface. |
|
 Matthew Wampler University of Virginia  |
Fragmentation and Novel Prethermal Dynamical Phases in Disordered, Strongly-Interacting Floquet SystemsWe explore how interactions can facilitate classical-like dynamics in Floquet models with sequentially activated hopping. Specifically, we add local and short range interaction terms to classes of Floquet Hamiltonians and ask for conditions ensuring the evolution acts as a permutation on initial local number Fock states. We show that at certain values of hopping and interactions, determined by a set of Diophantine equations, such evolution can be realized. When only a subset of the Diophantine equations is satisfied the Hilbert space can be fragmented into frozen states, states obeying cellular automata like evolution, and subspaces where evolution mixes Fock states and is associated with eigenstates exhibiting high entanglement entropy and level repulsion. When disorder is added to these systems, the dynamics may be stabilized in regions of parameter space away from these special parameter values - via k-body (or many-body) localization - to create new families of interesting phases. These families of phases also include phases already of current interest such as discrete time crystals and (correlation-induced) anomalous Floquet topological insulators. |
|
 Hong-Yi Wang Institute for Advanced Study, Tsinghua University  |
Amoeba formulation of the non-Hermitian skin effect in higher dimensionsThe non-Hermitian skin effect (NHSE) is a phenomenon that occurs in non-Hermitian lattice systems, in which eigenstates are massively squeezed to the boundary. A series of approaches, collectively known as the non-Bloch band theory, has provided systematic understanding of NHSE in 1D. However, it does not generalize naturally to higher dimensions. Although easy to confirm the existence of NHSE in higher dimensions, quantitatively understanding it remains challenging. In our recent works, we propose a universal solution to the NHSE under open boundary condition in any spatial dimensions (arXiv: 2212.11743), borrowing the concept of amoeba from algebraic geometry. With the amoeba formulation, we determine core quantities such as the density of states, Green’s function, generalized Brillouin zone and band topological invariants. We show that the “amoebic spectrum” is the unique stable eigenvalue spectrum against disorder. We also address possible geometry and boundary dependence of the spectrum. Although these cases deviate from the universal amoebic spectrum, they can be understood under the same framework. |
|
 Zack Weinstein University of California, Berkeley  |
Scrambling Transition in a Radiative Random Unitary CircuitWe study quantum information scrambling in a random unitary circuit that exchanges qubits with an environment at a rate p. As a result, initially localized quantum information not only spreads within the system, but also spills into the environment. Using the out-of-time-order correlator (OTOC) to characterize scrambling, we find a nonequilibrium phase transition in the directed percolation universality class at a critical swap rate pc: for p < p_c the ensemble-averaged OTOC exhibits ballistic growth with a tunable light cone velocity, while for p > p_c the OTOC fails to percolate within the system and vanishes uniformly within a finite timescale, indicating that all local operators are rapidly swapped into the environment. To elucidate its information-theoretic consequences, we demonstrate that the transition in operator spreading coincides with a transition in an observer’s ability to decode the system’s initial quantum information from the swapped-out, or “radiated,” qubits. We present a simple decoding scheme which recovers the system’s initial information with perfect fidelity in the nonpercolating phase, and with continuously decreasing fidelity with decreasing swap rate in the percolating phase. Depending on the initial state of the swapped-in qubits, we further observe a corresponding entanglement transition in the coherent information from the system into the radiated qubits. |
|
 Melissa Will Technical University of Munich  |
Hilbert Space Fragmentation and Hybrid Hydrodynamics in a Bose Hubbard ModelQuantum many-body systems out of equilibrium can exhibit very rich and exciting phenomena. A particularly relevant question is whether and how a quantum system thermalizes under its own unitary evolution. In this context, three classes of systems can be distinguished: ergodic, localized and intermediate regimes exhibiting quantum many-body scars. We consider a Bose Hubbard model on a square lattice in presence of a tilted field and demonstrate perturbatively the emergence of Hilbert space fragmentation (HSF) when fine tuning the on-site interactions. We investigate the quench dynamics of this system and find that the relaxation dynamics strongly depends on the chosen initial state—which we interpret as a signature of HSF. Furthermore, we identify point like excitations on top of certain frozen states, for which we analyze their dynamics using a cellular automaton. |
|
 Mingru Yang Max Planck Institute for Quantum Optics  |
Detecting emergent continuous internal symmetries at quantum criticalityNew or enlarged symmetries can emerge at the low-energy spectrum of a Hamiltonian that does not possess the symmetries, if the symmetry breaking terms in the Hamiltonian are irrelevant under the renormalization group flow. In this letter, we propose a tensor network based algorithm to numerically extract lattice operator approximation of the emergent conserved currents from the ground state of any quantum spin chains, without the necessity to have prior knowledge about its low-energy effective field theory. Our results for the spin-1/2 J-Q Heisenberg chain and a one-dimensional version of the deconfined quantum critical points (DQCP) demonstrate the power of our method to obtain the emergent lattice Kac-Moody generators. It can also be viewed as a way to find the local integrals of motion of an integrable model and the local parent Hamiltonian of a critical gapless ground state. |
|
 Bingtian Ye Harvard University  |
Universal Theory of Spin SqueezingQuantum metrology makes use of many-body entangled states to perform measurements with greater precision than would be possible using only classically correlated particles. Discerning states suitable for quantum metrology is a delicate task: nearly all states in Hilbert space are highly entangled, but nearly none of them exhibit the structured entanglement required for enhanced sensing. Identifying universal principles for finding metrologically useful states remains a long-standing challenge, especially in the context of efficiently preparing such states from unentangled product states. One such principle stems from the observation that the metrological gain from a pure state is fundamentally connected to spontaneous symmetry breaking. In this work, we apply this principle to the case of U(1) symmetry breaking and provide extensive numerical and analytical evidence for the following conjecture: Finite-temperature easy-plane ferromagnetism (i.e. XY magnets) enables scalable spin squeezing via quench dynamics. In particular, we establish a phase diagram for spin-squeezing, and demonstrate that tthe phase transition precisely coincides with the phase boundary for finite-temperature XY order. Moreover, we show that the squeezing manifests a novel scaling with system size that leads to a sensitivity ∼N^{-7/10}, in between the standard quantum limit ∼N^{-1/2} and the Heisenberg limit ∼N^{-1}. In addition, we also present an experimental observation of scalable spin squeezing in a Rydberg atom tweezer array. |
|
 Yicheng Zhang University of Oklahoma  |
Observation of hydrodynamization and local prethermalization in 1D Bose gasesHydrodynamics accurately describe relativistic heavy-ion collision experiments well before local thermal equilibrium is established. This unexpectedly rapid onset of hydrodynamics—which takes place on the fastest available timescale—is called hydrodynamization. It occurs when an interacting quantum system is quenched with an energy density that is much greater than its ground-state energy density. During hydrodynamization, energy gets redistributed across very different energy scales. Hydrodynamization precedes local equilibration among momentum modes, which is local prethermalization to a generalized Gibbs ensemble in nearly integrable systems or local thermalization in non-integrable systems. Although many theories of quantum dynamics postulate local prethermalization, the associated timescale has not been studied experimentally. Here we use an array of one-dimensional Bose gases to directly observe both hydrodynamization and local prethermalization. After we apply a Bragg scattering pulse, hydrodynamization is evident in the fast redistribution of energy among distant momentum modes, which occurs on timescales associated with the Bragg peak energies. Local prethermalization can be seen in the slower redistribution of occupation among nearby momentum modes. We find that the timescale for local prethermalization in our system is inversely proportional to the momenta involved. During hydrodynamization and local prethermalization, existing theories cannot quantitatively model our experiment. Exact theoretical calculations in the Tonks–Girardeau limit show qualitatively similar features. |
|
 Yi-Neng Zhou Institute for Advance Study, Tsinghua University  |
Universal Properties of the Spectral Form Factor in Open Quantum SystemsThe spectral form factor (SFF) can probe the eigenvalue statistic at different energy scales as its time variable varies. In closed quantum chaotic systems, the SFF exhibits a universal dip-ramp-plateau behavior, which reflects the spectrum rigidity of the Hamiltonian. In this work, we explore the universal properties of SFF in open quantum systems. We find that in open systems the SFF first decays exponentially, followed by a linear increase at some intermediate time scale, and finally decreases to a saturated plateau value. We derive universal relations between (1) the early-time decay exponent and Lindblad operators; (2) the long-time plateau value and the number of steady states. We also explain the effective field theory perspective of universal behaviors. We verify our theoretical predictions by numerically simulating the Sachdev-Ye-Kitaev (SYK) model, random matrix theory (RMT), and the Bose-Hubbard model. |

